
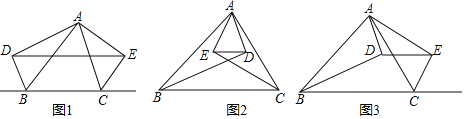
【题目】已知,△ABC,AD⊥BD于点D,AE⊥CE于点E,连接DE.
(1)如图1,若BD,CE分别为△ABC的外角平分线,求证:DE=![]() (AB+BC+AC).
(AB+BC+AC).
(2)如图2,若BD,CE分别为△ABC的内角平分线,(1)中的结论成立吗?若成立请说明理由;若不成立,请猜想出新的结论并证明;
(3)如图3,若BD,CE分别为△ABC的一个内角和一个外角的平分线,AB=8,BC=10,AC=7,请直接写出DE的长为______.
【答案】(1)证明见解析;(2)不成立.DE=![]() (AB+AC﹣BC),证明见解析;(3)4.5.
(AB+AC﹣BC),证明见解析;(3)4.5.
【解析】
(1)根据全等三角形的判定与性质,可得AB与BK,AC与CH的关系,根据等腰三角形的性质,可得AD与DK的关系,AE与EH的关系,根据三角形中位线的性质,可得答案;(2)都是内角平分线时,可根据等腰三角形三线合一的特点来求解,由于DB平分∠ABC,且AD⊥BD,如果延长AD交BC于K,那么三角形ABK就是个等腰三角形,AD=DK,如果延长AE到H,那么同理可证AG=GH,AC=CH,那么DE就是三角形AHK的中位线,DE就是HK的一半,而HK=BK﹣BH=BK﹣(BC﹣CH),由于BK=AB,CH=AC,那么可得出DE=![]() (AB+AC﹣BC);(3)证法同(1),先根据题目给出的求法,得出GD是AC的一半,然后按(2)的方法,通过延长AF来得出DF是(BC﹣AB)的一半,由此可得出DE=
(AB+AC﹣BC);(3)证法同(1),先根据题目给出的求法,得出GD是AC的一半,然后按(2)的方法,通过延长AF来得出DF是(BC﹣AB)的一半,由此可得出DE=![]() (BC+AC﹣AB),由此即可解决问题.
(BC+AC﹣AB),由此即可解决问题.
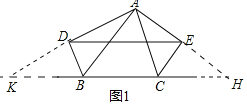
(1)证明:如图1,分别延长AE、AD交BC于H、K,
在△BAD和△BKD中,
∵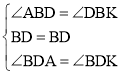 ,
,
∴△BAD≌△BKD(ASA),
∴AD=KD,AB=KB,
同理可证,AE=HE,AC=HC,
∴DE=![]() HK,
HK,
又∵HK=BK+BC+CH=AB+BC+AC,
∴DE=![]() (AB+AC+BC);
(AB+AC+BC);
(2)解:结论不成立.DE=![]() (AB+AC﹣BC).
(AB+AC﹣BC).
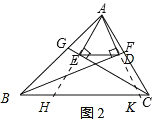
理由:如图2,分别延长AE、AD交BC于H、K,
在△BAD和△BKD中,
∵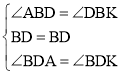 ,
,
∴△BAD≌△BKD(ASA),
∴AD=KD,AB=KB,
同理可证,AE=HE,AC=HC,
∴DE=![]() HK,
HK,
又∵HK=BK﹣BH=AB+AC﹣BC,
∴DE=![]() (AB+AC﹣BC).
(AB+AC﹣BC).
(3)解:分别延长AE、AD交BC或延长线于H、K,
在△BAD和△BKD中,
∵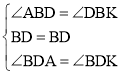 ,
,
∴△BAD≌△BKD(ASA),
∴AD=KD,AB=KB
同理可证,AE=HE,AC=HC,
∴DE=![]() KH
KH
又∵KH=BC﹣BK+HC=BC+AC﹣AB.
∴DE=![]() (BC+AC﹣AB),
(BC+AC﹣AB),
∵AB=8,BC=10,AC=7,
∴DE=![]() (10+7﹣8)=4.5,
(10+7﹣8)=4.5,
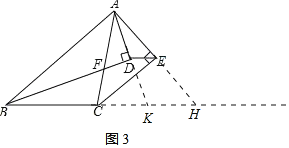
故答案为4.5.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
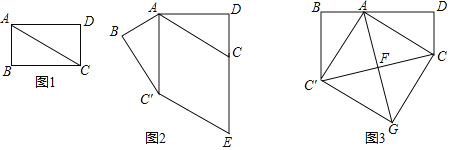
【题目】如图1,将矩形纸片ABCD沿AC剪开,得到△ABC和△ACD.
(1)将图1中的△ABC绕点A顺时针旋转∠α,使∠α=∠BAC,得到图2所示的△ABC′,过点C′作C′E∥AC,交DC的延长线于点E,试判断四边形ACEC′的形状,并说明理由.
(2)若将图1中的△ABC绕点A顺时针旋转,使B,A,D在同一条直线上,得到图3所示的△ABC′,连接CC′,过点A作AF⊥CC′于点F,延长AF至点G,使FG=AF,连接CG,C′G,试判断四边形ACGC′的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.

根据以上信息解决下列问题:
(1)![]() ,
,![]() ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的![]() 名学生中恰好有
名学生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,以AB为一边作等边△ABE,使点E落在正方形ABCD的内部,连接AC交BE于点F,连接CE、DE,则下列说法中:①△ADE≌△BCE;②∠ACE=30°;③AF=![]() CF;④
CF;④ ![]() =2+
=2+![]() ,其中正确的有( )
,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com