
����Ŀ����2017�Ĵ�ʡ�����У���10�⣬3�֣���֪����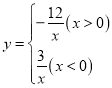 ��ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�
��ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�
������M1��x1��y1����M2��x2��y2����ͼ���ϣ���x1��x2��0����y1��y2��
�ڵ���P����Ϊ��0����3��ʱ����AOB�ǵ��������Σ�
�����۵�P��ʲôλ�ã�ʼ����S��AOB=7.5��AP=4BP��
�ܵ���P�ƶ���ʹ��AOB=90��ʱ����A������Ϊ��![]() ��
��![]() ����
����
������ȷ�Ľ��۸���Ϊ��������
A.1B.2C.3D.4
���𰸡�C
��������
����ٴ���x1��x2��0������y��x���������С����y1��y2���ʢٴ���
����ȷ����P��0����3������B����1����3����A��4����3������AB=5��OA=![]() =5����AB=AO�����AOB�ǵ��������Σ��ʢ���ȷ��
=5����AB=AO�����AOB�ǵ��������Σ��ʢ���ȷ��
����ȷ����P��0��m������B��![]() ��m����A����
��m����A����![]() ��m������PB=��
��m������PB=��![]() ��PA=��
��PA=��![]() ����PA=4PB����SAOB=S��OPB+S��OPA=
����PA=4PB����SAOB=S��OPB+S��OPA=![]() =7.5���ʢ���ȷ��
=7.5���ʢ���ȷ��
����ȷ����P��0��m������B��![]() ��m����A����
��m����A����![]() ��m������PB=��
��m������PB=��![]() ��PA=��
��PA=��![]() ��OP=��m���ߡ�AOB=90�㣬��OPB=��OPA=90�㣬���BOP+��AOP=90�㣬��AOP+��OPA=90�㣬���BOP=��OAP�����OPB�ס�APO����
��OP=��m���ߡ�AOB=90�㣬��OPB=��OPA=90�㣬���BOP+��AOP=90�㣬��AOP+��OPA=90�㣬���BOP=��OAP�����OPB�ס�APO����![]() ����OP2=PBPA����m2=��
����OP2=PBPA����m2=��![]() ����
����![]() ������m4=36����m��0����m=��
������m4=36����m��0����m=��![]() ����A��
����A��![]() ����
����![]() �����ʢ���ȷ����ڢۢ���ȷ����ѡC��
�����ʢ���ȷ����ڢۢ���ȷ����ѡC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
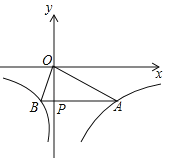
����Ŀ����֪AB�ǡ�O��ֱ����C��Բ�ϵĵ㣬D���Ż�ABC���е㣮
��1������AOC��100�������D�Ķ���Ϊ�� ������A�Ķ���Ϊ�� ����
��2����֤����ADC��2��DAB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
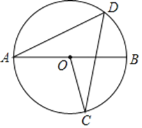
����Ŀ����ͼ��Բ�ڽ��ı���ABDC��AB����O��ֱ����OD��BC��E��
��1����֤����BCD=��CBD��
��2����BE=4��AC=6����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ��ֱ������ϵ��������������y![]() ��b��0������κ���y��ax2+bx��a��0����ͼ������ǣ�������
��b��0������κ���y��ax2+bx��a��0����ͼ������ǣ�������
A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
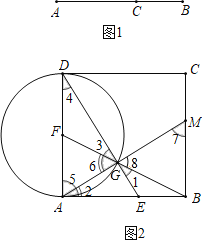
����Ŀ���Ķ����в��ϣ������Ӧ��ѧϰ����:��ͼ��1�����߶�AB����һ��C��C��AB��ΪAC��BC�����߶Σ�����AC��BC����AC��BC��AB�����ϵAC2��BCAB�����C�����߶�AB�Ļƽ�ָ�㣬��ʱ![]() ��
��![]() ��0.618�����ǰ�
��0.618�����ǰ�![]() �����ƽ�ָ��������ǿ��Ը���ͼ��2����ʾ���������ҵ��߶�AB�Ļƽ�ָ�㣬��������Ͳ���֤���������£�
�����ƽ�ָ��������ǿ��Ը���ͼ��2����ʾ���������ҵ��߶�AB�Ļƽ�ָ�㣬��������Ͳ���֤���������£�
��һ������ABΪ����������ABCD��
�ڶ�������ADΪֱ������F��
������������BF���F���ڵ�G��
���IJ�������DG���ӳ���AB���ڵ�E����E�����߶�AB�Ļƽ�ָ�㣮
֤��������AG���ӳ�����BC���ڵ�M��
��ADΪ��F��ֱ����
���AGD��90����
��FΪAD���е㣬
��DF��FG��AF��
���3����4����5����6��
�ߡ�2+��5��90������5+��4��90����
���2����4����3����1��
�ߡ�EBG����GBA��
���EBG�ס�GBA��
��![]() ��
��![]() ��
��
��BG2��BEAB��
����
��1�������������������벿��֤�����̣���ʣ���֤�����̲�������������ʾ��֤��BM��BG��AE��
��2����ѡ����һ�־��й㷺Ӧ�ü�ֵ����ѧ��������ѡ������һ��0.618��Ӧ���˻ƽ�ָ�����Ϊ��ѡ�����ռ�������Ҫ�����ҹ���ѧ������ �����������ѡ�����ĸ���ţ�
A������
B���¾���
C���ղ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
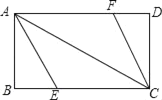
����Ŀ��ͬѧ�ŷ���һ�ų�18cm����12cm����ֽƬ�۳�һ�����Σ����ؾ��εĶԽ���AC�۳���CAE����DAC����ACF����ACB�ķ����õ��ı���AECF����ͼ����
��1��֤�����ı���AECF�����Σ�
��2��������AECF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
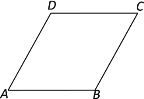
����Ŀ����ͼ����һ����ֽƬABCD����A��60������������ֽƬ�۵���ʹ��Aǡ����CD���е�E�غϣ��ۺ�ΪFG����F��G�ֱ��ڱ�AB��AD�ϣ�����EF����ôcos��EFB��ֵΪ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�������ѧ���μӡ�����֪ʶ�������ɼ���������������˲��ֲ���ѧ���ijɼ������������������µ�ͳ�Ʊ���ͳ��ͼ����ͼ��ʾ�������ͼ����Ϣ����������⣺
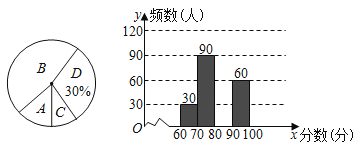
��� | �����Σ��֣� | Ƶ�� |
A�� | 60��x��70 | 30 |
B�� | 70��x��80 | 90 |
C�� | 80��x��90 | m |
D�� | 90��x��100 | 60 |
��1�����ε����������Ϊ�� ���ˣ�
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����A��ѧ����ƽ������65�֣�B��ѧ����ƽ������75�֣�C��ѧ����ƽ������85�֣�D��ѧ����ƽ������95�֣�������Ʋμӱ��β��Ե�ͬѧ��ƽ���ɼ��Ƕ��ٷ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+5��ͼ���뷴��������![]() ��k��0���ڵ�һ����ͼ����A��1��n����B���㣮
��k��0���ڵ�һ����ͼ����A��1��n����B���㣮

��1�����������Ľ���ʽ����B���ꣻ
��2���ڵ�һ�����ڣ���һ�κ���y����x��5��ֵ���ڷ���������![]() ��k��0����ֵʱ��д���Ա���x��ȡֵ��Χ��
��k��0����ֵʱ��д���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com