
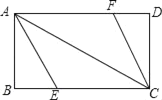
【题目】同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).
(1)证明:四边形AECF是菱形;
(2)求菱形AECF的面积.
【答案】(1)详见解析;(2)156.
【解析】
(1)先证明四边形AECF是平行四边形,再证明AF=CE即可.
(2)在RT△ABE中利用勾股定理求出BE、AE,再根据S菱形AECF=S矩形ABCD﹣S△ABE﹣S△DFC求出面积即可.
(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠FAC=∠ACE,
∵∠CAE=∠DAC,∠ACF=∠ACB,
∴∠EAC=∠ACF,
∴AE∥CF,∵AF∥EC,
∴四边形AECF是平行四边形,
∵∠FAC=∠FCA,
∴AF=CF,
∴四边形AECF是菱形.
(2)解:∵四边形AECF是菱形,
∴AE=EC=CF=AF,设菱形的边长为a,
在RT△ABE中,∵∠B=90°,AB=12,AE=a,BE=18﹣a,
∴a2=122+(18﹣a)2,
∴a=13,
∴BE=DF=5,AF=EC=13,
∴S菱形AECF=S矩形ABCD﹣S△ABE﹣S△DFC=216﹣30﹣30=156cm2.



 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2![]() ,∠BAC=120°,D为BC边上的点,将DA绕D点逆时针旋转120°得到DE.
,∠BAC=120°,D为BC边上的点,将DA绕D点逆时针旋转120°得到DE.
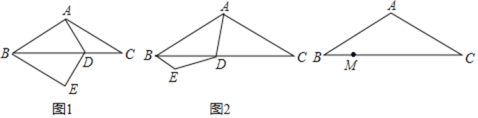
(1)如图1,若AD=DC,则BE的长为 ,BE2+CD2与AD2的数量关系为 ;
(2)如图2,点D为BC边山任意一点,线段BE、CD、AD是否依然满足(1)中的关系,试证明;
(3)M为线段BC上的点,BM=1,经过B、E、D三点的圆最小时,记D点为D1,当D点从D1处运动到M处时,E点经过的路径长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
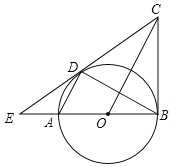
【题目】如图,AB为![]() 的直径,BC为
的直径,BC为![]() 的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是
的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是![]() 的切线;②
的切线;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
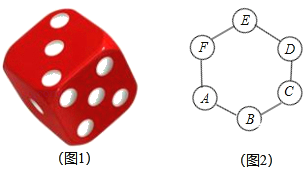
【题目】元旦期间,九年级某班六位同学进行跳圈游戏,具体过程如下:图1所示是一枚质地均匀的正方体骰子,骰子的六个面上的点数分别是1,2,3,4.5,6,如图2,正六边形ABCDEF的顶点处各有一个圈.跳圈游戏的规则为:游戏者每投掷一次骰子,假骰子向上的一面上的点数是几,就沿着正六边形的边逆时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就逆时针连续跳3个边长,落到圈D;若第二次掷得2.就从图D开始逆时针连续起跳2个边长,落到圈F…,设游戏者从圈A起跳
(1)小明随机掷一次骰子,求落回到圈A的概率P1;
(2)小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈A的概率P2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017四川省达州市,第10题,3分)已知函数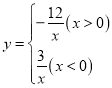 的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A,B两点,连接OA、OB.下列结论:
①若点M1(x1,y1),M2(x2,y2)在图象上,且x1<x2<0,则y1<y2;
②当点P坐标为(0,﹣3)时,△AOB是等腰三角形;
③无论点P在什么位置,始终有S△AOB=7.5,AP=4BP;
④当点P移动到使∠AOB=90°时,点A的坐标为(![]() ,
,![]() ).
).
其中正确的结论个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
材料1 若一元二次方程ax2+bx+c=0(a≠0)的两个根为x1,x2则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() .
.
材料2 已知实数m,n满足m2﹣m﹣1=0,n2﹣n﹣1=0,且m≠n,求![]() 的值.
的值.
解:由题知m,n是方程x2﹣x﹣1=0的两个不相等的实数根,根据材料1得m+n=1,mn=﹣1,所以![]() =﹣3.
=﹣3.
根据上述材料解决以下问题:
(1)材料理解:一元二次方程5x2+10x﹣1=0的两个根为x1,x2,则x1+x2= ,x1x2= .
(2)类比探究:已知实数m,n满足7m2﹣7m﹣1=0,7n2﹣7n﹣1=0,且m≠n,求m2n+mn2的值:
(3)思维拓展:已知实数s、t分别满足19s2+99s+1=0,t2+99t+19=0,且st≠1.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
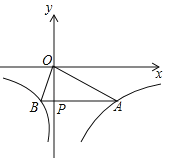
【题目】已知:如图,在△ABC中,AB=AC,点D、E分别在边BC、DC上,AB2 =BE · DC ,DE:EC=3:1 ,F是边AC上的一点,DF与AE交于点G.
(1)找出图中与△ACD相似的三角形,并说明理由;
(2)当DF平分∠ADC时,求DG:DF的值;
(3)如图,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的面积等分线.
问题探究
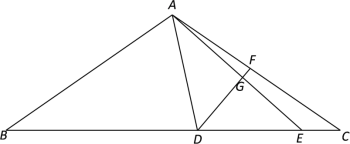
(1)如图1,△ABC中,点M是AB边的中点,请你过点M作△ABC的一条面积等分线;
(2)如图2,在四边形ABCD中,AD∥BC,CD⊥AD,AD=2,CD=4,BC=6,点P是AB的中点,点Q在CD上,试探究当CQ的长为多少时,直线PQ是四边形ABCD的一条面积等分线;
问题解决
(3)如图3,在平面直角坐标系中,矩形ABCD是某公司将要筹建的花园示意图,A与原点重合,D、B分别在x轴、y轴上,其中AB=3,BC=5,出入口E在边AD上,且AE=1,拟在边BC、AB、CD、上依次再找一个出入口F、G、H,沿EF、GH修两条笔直的道路(路的宽度不计)将花园分成四块,在每一块内各种植一种花草,并要求四种花草的种植面积相等.请你求出此时直线EF和GH的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
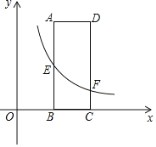
【题目】如图,矩形ABCD的两边AD,AB的长分别为3,8,E是AB的中点,反比例函数y=![]() 的图象经过点E,与CD交于点F.
的图象经过点E,与CD交于点F.
(1)若点C坐标为(6,0),求m的值及图象经过D,E两点的直线解析式;
(2)若DF﹣DE=2,求反比例函数的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com