
【题目】如图,△ABC内接于⊙O,AB=AC,∠ABC=72°,过点A作BC的平行线与∠ABC的平分线交于点D,BD交AC于点E,交⊙O于点F,连接AF.
(1)求证:AD是⊙O的切线;
(2)已知BC=2,求EF的长.

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接AO,OB,求出∠OAD=90°即可;
(2)证得△AEF≌△BCE,得出EF=CE,设EF=EC=x,则AC=2+x,证得△ABC∽△BEC,根据相似三角形的性质得出关于x的方程,解方程即可.
(1)证明:连接AO、BO、CO,
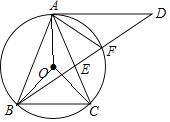
∵AB=AC,∠ABC=72°,
∴∠ABC=∠ACB=72°,
∴∠BAC=36°,
在△ABO和△ACO中
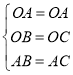 ,
,
∴△ABO≌△ACO(SSS),
∴∠OAC=![]() ∠BAC=18°,
∠BAC=18°,
∵AD∥BC,
∴∠DAC=∠ACB=72°,
∴∠OAD=∠OAC+∠DAC=18°+72°=90°,
∴AD是⊙O的切线;
(2)解:∵∠BAC=∠ABD=36°,
∴AE=BE,
∵∠DBC=36°∠ACB=72°,
∴∠BEC=72°,
∴BE=BC=2,
∴AE=BC,
在△BCE和△AFE中
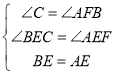 ,
,
∴△AEF≌△BCE(AAS),
∴EF=CE,
设EF=EC=x,则AC=2+x,
∵∠ABC=∠BEC=72°,∠ACB=∠BCE,
∴△ABC∽△BEC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得x=![]() ﹣1或﹣1﹣
﹣1或﹣1﹣![]() (舍去),
(舍去),
∴EF=![]() ﹣1.
﹣1.
故答案为:(1)详见解析;(2)![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )
A. a≤﹣1或![]() ≤a<
≤a<![]() B.
B. ![]() ≤a<
≤a<![]()
C. a≤![]() 或a>
或a>![]() D. a≤﹣1或a≥
D. a≤﹣1或a≥![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们设计了一个重复抛掷的实验:全班48人分为8个小组,每组抛掷同一型号的一枚瓶盖300次,并记录盖面朝上的次数,下表是依次累计各小组的实验结果.
1组 | 1~2组 | 1~3组 | 1~4组 | 1~5组 | 1~6组 | 1~7组 | 1~8组 | |
盖面朝上次数 | 165 | 335 | 483 | 632 | 801 | 949 | 1122 | 1276 |
盖面朝上频率 | 0.550 | 0.558 | 0.537 | 0.527 | 0.534 | 0.527 | 0.534 | 0.532 |
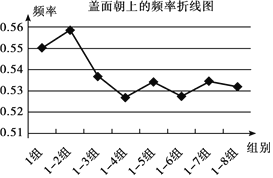
根据实验,你认为这一型号的瓶盖盖面朝上的概率为____,理由是:____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
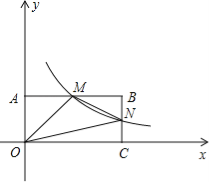
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
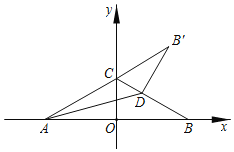
【题目】如图,直线y=![]() x+1分别交x轴、y轴于点A、C,点B是点A关于y的对称点,点D是线段BC上一点,把△ABD沿AD翻折使AB落在射线AC上,得△AB'D,则△ABC与△AB'D重叠部分的面积为( )
x+1分别交x轴、y轴于点A、C,点B是点A关于y的对称点,点D是线段BC上一点,把△ABD沿AD翻折使AB落在射线AC上,得△AB'D,则△ABC与△AB'D重叠部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+ ![]() )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+ ![]() 的自变量x的取值范围是x>0,下表是y与x的几组对应值.
的自变量x的取值范围是x>0,下表是y与x的几组对应值.

① 写出m的值;
②画出该函数图象,结合图象,得出当x=________时,y有最小值,y最小=________;
提示:在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.试用配方法求函数y=x+ ![]() (x>0)的最小值,解决问题(2).
(x>0)的最小值,解决问题(2).
(2)【解决问题】
直接写出“问题情境”中问题的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
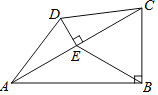
【题目】如图,在四边形ABCD中,∠ABC=90°,DE⊥AC于点E,且AE=CE,DE=5,EB=12.
(1)求AD的长;
(2)若∠CAB=30°,求四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 经过点A(-1,0)和点B(4,5).
经过点A(-1,0)和点B(4,5).
(1)求该抛物线的函数表达式.
(2)求直线AB关于x轴对称的直线的函数表达式.
(3)点P是x轴上的动点,过点P作垂直于x轴的直线l,直线l与该抛物线交于点M,与直线AB交于点N.当PM < PN时,求点P的横坐标![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A,B,与y轴交于点C(0,2),直线
与x轴交于A,B,与y轴交于点C(0,2),直线![]() 经过点A,C.
经过点A,C.
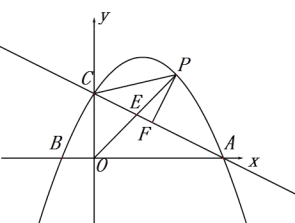
(1)求抛物线的解析式;
(2)点P为直线AC上方抛物线上一动点;
①连接PO,交AC于点E,求![]() 的最大值;
的最大值;
②过点P作PF⊥AC,垂足为点F,连接PC,是否存在点P,使△PFC中的一个角等于∠CAB的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com