练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

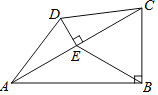
    【题目】如图，在四边形ABCD中，∠ABC＝90°，DE⊥AC于点E，且AE＝CE，DE＝5，EB＝12．

    （1）求AD的长；

    （2）若∠CAB＝30°，求四边形ABCD的周长．

    【答案】（1）13；（2）38+．

    【解析】

    （1）根据等腰三角形的性质和勾股定理即可得到结论；
    （2）解直角三角形求出各边的长，于是得到结论．

    解：（1）∵∠ABC＝90°，AE＝CE，EB＝12，

    ∴EB＝AE＝CE＝12．

    ∵DE⊥AC，DE＝5，

    ∴在Rt△ADE中，

    由勾股定理得AD＝＝＝13；

    （2）∵在Rt△ABC中，∠CAB＝30°，AC＝AE+CE＝24，

    ∴BC＝12，AB＝ACcos30°＝，

    ∵DE⊥AC，AE＝CE，

    ∴AD＝DC＝13，

    ∴四边形ABCD的周长为AB+BC+CD+AD＝38+．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

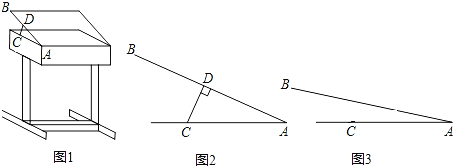
    【题目】某课桌生产厂家研究发现，倾斜12°﹣24°的桌面有利于学生保持躯体自然姿势．根据这一研究，厂家决定将水平桌面做成可调节角度的桌面．新桌面的设计图如图1所示，AB可绕点A旋转，在点C处安装一根可旋转的支撑臂CD，AC＝30cm．

    （1）如图2，当∠BAC＝24°时，CD⊥AB，求支撑臂CD的长．

    （2）如图3，当∠BAC＝12°，求AD的长（结果保留根号）．

    [参考数据：sin24°＝0.40，cos24°＝0.91，tan24°＝0.46，sin12°＝0.20]

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知是的函数，自变量的取值范围是的全体实数，如表是与的几组对应值．

    小华根据学习函数的经验，利用上述表格所反映出的与之间的变化规律，对该函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：

    （1）从表格中读出，当自变量是﹣2时，函数值是　 　；

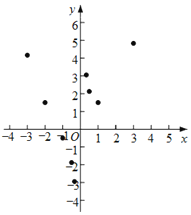
    （2）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；

    （3）在画出的函数图象上标出时所对应的点，并写出　 　．

    （4）结合函数的图象，写出该函数的一条性质：　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC内接于⊙O，AB＝AC，∠ABC＝72°，过点A作BC的平行线与∠ABC的平分线交于点D，BD交AC于点E，交⊙O于点F，连接AF．

    （1）求证：AD是⊙O的切线；

    （2）已知BC＝2，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

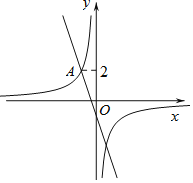
    【题目】如图，在平面直角坐标系xOy中，直线与双曲线相交于点．

    求双曲线的表达式；

    过动点且垂直于x轴的直线与直线及双曲线的交点分别为B和C，当点B位于点C下方时，求出n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，过原点O的直线l1与双曲线的一个交点为A（1，m）．

    （1）求直线l1的表达式；

    （2）过动点P（n，0）（n＞0）且垂直于x轴的直线与直线l1和双曲线的交点分别为B，C，当点B位于点C上方时，直接写出n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】每年农历五月初五为端午节，中国民间历来有端午节吃粽子、赛龙舟的习俗．某班同学为了更好地了解某社区居民对鲜肉粽（A）豆沙粽（B）小枣粽（C）蛋黄粽（D）的喜爱情况，对该社区居民进行了随机抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）．

    分析图中信息，本次抽样调查中喜爱小枣粽的人数为________；若该社区有10000人，估计爱吃鲜肉粽的人数约为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

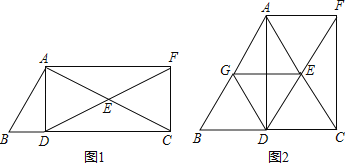
    【题目】在△ABC中，AD⊥BC于点D，点E为AC边的中点，过点A作AF∥BC，交DE的延长线于点F，连接CF．

    （1）如图1，求证：四边形ADCF是矩形；

    （2）如图2，当AB＝AC时，取AB的中点G，连接DG、EG，在不添加任何辅助线和字母的条件下，请直接写出图中所有的平行四边形（不包括矩形ADCF）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是平行四边形，点A(1，0)，B(3，1)，C(3，3)．反比例函数y＝ (x＞0)的图像经过点D，P是一次函数y＝kx＋3－3k(k≠0)的图像与该反比例函数图像的一个公共点．

    (1)求反比例函数的表达式；

    (2)通过计算说明一次函数y＝kx＋3－3k(k≠0)的图像一定经过点C；

    (3)对于一次函数y＝kx＋3－3k(k≠0)，当y随x的增大而增大时，确定点P的横坐标的取值范围(不必写出过程)．

    查看答案和解析>>

    同步练习册答案