
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y=![]() (x>0)的图像经过点D,P是一次函数y=kx+3-3k(k≠0)的图像与该反比例函数图像的一个公共点.
(x>0)的图像经过点D,P是一次函数y=kx+3-3k(k≠0)的图像与该反比例函数图像的一个公共点.
(1)求反比例函数的表达式;
(2)通过计算说明一次函数y=kx+3-3k(k≠0)的图像一定经过点C;
(3)对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).

【答案】y=![]() ;略;
;略;![]() <a<3.
<a<3.
【解析】
(1)由B(3,1),C(3,3)得到BC⊥x轴,BC=2,根据平行四边形的性质得AD=BC=2,而A点坐标为(1,0),可得到点D的坐标为(1,2),然后把D(1,2)代入y=![]() 即可得到m=2,从而可确定反比例函数的解析式;
即可得到m=2,从而可确定反比例函数的解析式;
(2)把x=3代入y=kx+3-3k(k≠0)得到y=3,即可说明一次函数y=kx+3-3k(k≠0)的图象一定过点C;
(3)设点P的横坐标为a,由于一次函数y=kx+3-3k(k≠0)过C点,并且y随x的增大而增大时,则P点的纵坐标要小于3,横坐标要小于3,当纵坐标小于3时,由y=![]() 得到a>
得到a>![]() ,于是得到a的取值范围.
,于是得到a的取值范围.
(1)∵四边形ABCD是平行四边形,
∴AD=BC,
∵B(3,1),C(3,3),
∴BC⊥x轴,AD=BC=2,
而A点坐标为(1,0),
∴点D的坐标为(1,2).
∵反比例函数y=![]() (x>0)的函数图象经过点D(1,2),
(x>0)的函数图象经过点D(1,2),
∴2=![]()
∴m=2
∴反比例函数的解析式为y=![]() ;
;
(2)当x=3时,y=kx+3-3k=3k+3-3k=3,
∴一次函数y=kx+3-3k(k≠0)的图象一定过点C;
(3)设点P的横坐标为a,
则a的范围为![]() <a<3.
<a<3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将正方形 ABCD (如图 1)作如下划分:
第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
第2次划分:将图2 左上角正方形AEMH再作划分,得图3,则图3 中共有9个正方形;
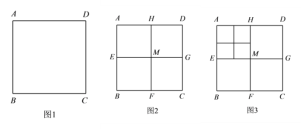
(1)若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有 个正方形;
(2)继续划分下去,第几次划分后能有805个正方形?写出计算过程.
(3)按这种方法能否将正方形ABCD划分成有2015个正方形的图形?如果能,请算出是第几次划分,如果不能,需说明理由.
(4)如果设原正方形的边长为1,通过不断地分割该面积为1的正方形,并把数量关系和几何图形巧妙地结合起来,可以很容易得到一些计算结果,试着探究求出下面表达式的结果吧.
计算 ![]() .( 直接写出答案即可)
.( 直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】背景知识:
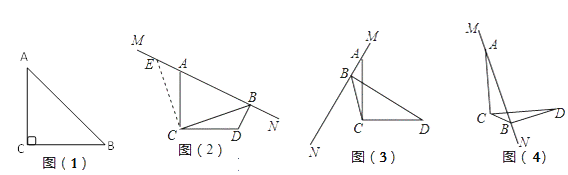
如图(2),在Rt△ABC中,∠ACB=90°,![]() ,则:
,则:![]() .
.
(1)解决问题:
如图(2),∠ACD = 90°,AC = DC,MN是过点A的直线,过点D作DB⊥MN于点B,连接CB,试探究线段BA、BC、BD之间的数量关系.
不妨过点C作CE⊥CB,与MN交于点E,易发现图中出现了一对全等三角形,即 ≌ ,由此可得线段BA、BC、BD之间的数量关系是: .
(2)类比探究:
将图(2)中的MN绕点A旋转到图(3)的位置,其它条件不变,试探究线段BA、BC、BD之间的数量关系,并证明.
(3)拓展应用:
将图(2)中的MN绕点A旋转到图(4)的位置,其它条件不变,若BD=2,BC=![]() ,则AB的长为 .
,则AB的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用114元从蔬菜批发市场购进黄瓜和土豆共40kg到菜市场去卖,黄瓜和土豆这天的批发价好零售价(单位:元/kg)如下表所示:
品名 | 批发价 | 零售价 |
黄瓜 | 2.4 | 4 |
土豆 | 3 | 5 |
(1)他当天购进黄瓜和土豆各多少千克?
(2)如果黄瓜和土豆全部卖完,他能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解密数学魔术:魔术师请观众心想一个数,然后将这个数按以下步骤操作:![]()
魔术师能立刻说出观众想的那个数.
(1)如果小玲想的数是-1,那么她告诉魔术师的结果应该是 ;
(2)如果小明想了一个数计算后,告诉魔术师结果为93,那么魔术师立刻说出小明想的那个数是 ;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数.若设观众心想的数为a,请通过计算解密这个魔术的奥妙.
查看答案和解析>>
科目:初中数学 来源: 题型:
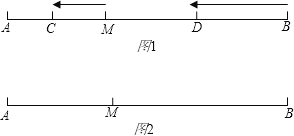
【题目】已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)
(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值.
(2)若点C、D运动时,总有MD=3AC,直接填空:AM= AB.
(3)在(2)的条件下,N是直线AB上一点,且AN-BN=MN,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
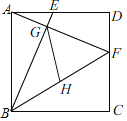
【题目】已知正方形ABCD的边长为4,点E,F分别在AD,DC上,AE=DF=1,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com