
【题目】在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是矩形;
(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).
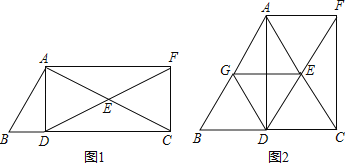
【答案】(1)见解析;(2)四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.
【解析】
(1)由△AEF≌△CED,推出EF=DE,又AE=EC,推出四边形ADCF是平行四边形,只要证明∠ADC=90°,即可推出四边形ADCF是矩形.
(2)根据三角形的中位线定理和平行四边形的判定即可找出图中的所有平行四边形.
(1)证明:∵AF∥BC,
∴∠AFE=∠EDC,
∵E是AC中点,
∴AE=EC,
在△AEF和△CED中,
 ,
,
∴△AEF≌△CED,
∴EF=DE,∵AE=EC,
∴四边形ADCF是平行四边形,
∵AD⊥BC,
∴∠ADC=90°,
∴四边形ADCF是矩形.
(2)∵线段DG、线段GE、线段DE都是△ABC的中位线,又AF∥BC,
∴AB∥DE,DG∥AC,EG∥BC,
∴四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】同学们设计了一个重复抛掷的实验:全班48人分为8个小组,每组抛掷同一型号的一枚瓶盖300次,并记录盖面朝上的次数,下表是依次累计各小组的实验结果.
1组 | 1~2组 | 1~3组 | 1~4组 | 1~5组 | 1~6组 | 1~7组 | 1~8组 | |
盖面朝上次数 | 165 | 335 | 483 | 632 | 801 | 949 | 1122 | 1276 |
盖面朝上频率 | 0.550 | 0.558 | 0.537 | 0.527 | 0.534 | 0.527 | 0.534 | 0.532 |
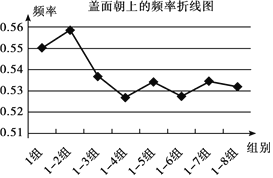
根据实验,你认为这一型号的瓶盖盖面朝上的概率为____,理由是:____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,DE⊥AC于点E,且AE=CE,DE=5,EB=12.
(1)求AD的长;
(2)若∠CAB=30°,求四边形ABCD的周长.
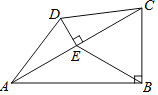
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 经过点A(-1,0)和点B(4,5).
经过点A(-1,0)和点B(4,5).
(1)求该抛物线的函数表达式.
(2)求直线AB关于x轴对称的直线的函数表达式.
(3)点P是x轴上的动点,过点P作垂直于x轴的直线l,直线l与该抛物线交于点M,与直线AB交于点N.当PM < PN时,求点P的横坐标![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市正在开展“太极拳进校园”活动,为了解学生太极拳的练习情况,随机抽取了部分学校学生进行问卷调查,将调查结果按照“![]() 每周练习6次或7次,
每周练习6次或7次,![]() 每周练习4次或5次,
每周练习4次或5次,![]() 每周练习2次或3次,
每周练习2次或3次,![]() 每周练习0次或1次”四类分别进行统计,并绘制了下列两幅尚不完整的统计图.
每周练习0次或1次”四类分别进行统计,并绘制了下列两幅尚不完整的统计图.
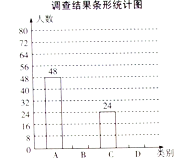
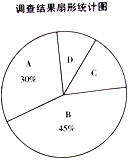
请根据图中信息,解答下列问题:
(1)此次共调查了___________名学生;
(2)在扇形统计图中,扇形![]() 的圆心角度数为__________;
的圆心角度数为__________;
(3)请将条形统计图补充完整;
(4)若该市约有30万名学生,请你估计每周练习太极拳不少于4次的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线l经过点A(﹣2,0)和点B(0,1),点M在x轴上,过点M作x轴的垂线交直线l于点C,若OM=2OA,则经过点C的反比例函数表达式为( )
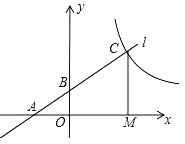
A.y=![]() B.y=
B.y=![]() C.y=
C.y=![]() D.y=
D.y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A,B,与y轴交于点C(0,2),直线
与x轴交于A,B,与y轴交于点C(0,2),直线![]() 经过点A,C.
经过点A,C.
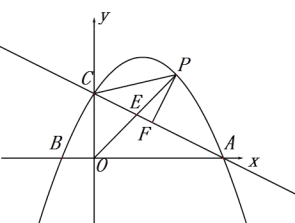
(1)求抛物线的解析式;
(2)点P为直线AC上方抛物线上一动点;
①连接PO,交AC于点E,求![]() 的最大值;
的最大值;
②过点P作PF⊥AC,垂足为点F,连接PC,是否存在点P,使△PFC中的一个角等于∠CAB的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C:y=ax2﹣2ax+3与直线l:y=kx+b交于A,B两点,且点A在y轴上,点B在x轴的正半轴上.
(1)求点A的坐标;
(2)若a=﹣1,求直线l的解析式;
(3)若﹣3<k<﹣1,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com