
【题目】在平面直角坐标系中,抛物线![]() 经过点A(-1,0)和点B(4,5).
经过点A(-1,0)和点B(4,5).
(1)求该抛物线的函数表达式.
(2)求直线AB关于x轴对称的直线的函数表达式.
(3)点P是x轴上的动点,过点P作垂直于x轴的直线l,直线l与该抛物线交于点M,与直线AB交于点N.当PM < PN时,求点P的横坐标![]() 的取值范围.
的取值范围.

【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据待定系数法,可得二次函数的解析式;
(2)根据待定系数法,可得AB的解析式,根据关于x轴对称的横坐标相等,纵坐标互为相反数,可得答案;
(3)根据PM<PN,可得不等式,利用绝对值的性质化简解不等式,可得答案.
(1)将A(﹣1,0),B(4,5)代入函数解析式,得:
![]() ,解得:
,解得:![]() ,抛物线的解析式为y=x2﹣2x﹣3;
,抛物线的解析式为y=x2﹣2x﹣3;
(2)设AB的解析式为y=kx+b,将A(﹣1,0),B(4,5)代入函数解析式,得:
![]() ,解得:
,解得:![]() ,直线AB的解析式为y=x+1,直线AB关于x轴的对称直线的表达式y=﹣(x+1),化简,得:y=﹣x﹣1;
,直线AB的解析式为y=x+1,直线AB关于x轴的对称直线的表达式y=﹣(x+1),化简,得:y=﹣x﹣1;
(3)设M(n,n2﹣2n﹣3),N(n,n+1),PM<PN,即|n2﹣2n﹣3|<|n+1|.
∴|(n+1)(n-3)|-|n+1|<0,∴|n+1|(|n-3|-1)<0.
∵|n+1|≥0,∴|n-3|-1<0,∴|n-3|<1,∴-1<n-3<1,解得:2<n<4.
故当PM<PN时,求点P的横坐标xP的取值范围是2<xP<4.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
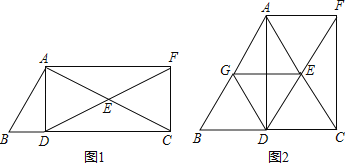
【题目】已知,在Rt△ABC中,∠B=90°,AB=![]() ,BC=3,在BC边上取两点E,F(点E在点F左侧),以EF为边作等边三角形DEF,使顶点D与E在边AC异侧,DE,DF分别交AC于点G,H,连结AD.
,BC=3,在BC边上取两点E,F(点E在点F左侧),以EF为边作等边三角形DEF,使顶点D与E在边AC异侧,DE,DF分别交AC于点G,H,连结AD.

(1)如图1,求证:DE⊥AC;
(2)如图2,若∠DAC=30°,△DEF的边EF在线段BC上移动.写出DH与BE的数量关系并证明;
(3)若30°<∠DAC<60°,△DEF的周长为m,则m的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,∠ABC=72°,过点A作BC的平行线与∠ABC的平分线交于点D,BD交AC于点E,交⊙O于点F,连接AF.
(1)求证:AD是⊙O的切线;
(2)已知BC=2,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过原点O的直线l1与双曲线![]() 的一个交点为A(1,m).
的一个交点为A(1,m).
(1)求直线l1的表达式;
(2)过动点P(n,0)(n>0)且垂直于x轴的直线与直线l1和双曲线![]() 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年农历五月初五为端午节,中国民间历来有端午节吃粽子、赛龙舟的习俗.某班同学为了更好地了解某社区居民对鲜肉粽(A)豆沙粽(B)小枣粽(C)蛋黄粽(D)的喜爱情况,对该社区居民进行了随机抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

分析图中信息,本次抽样调查中喜爱小枣粽的人数为________;若该社区有10000人,估计爱吃鲜肉粽的人数约为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是矩形;
(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在一个不透明的口袋中有4个形状、大小、材质完全相同的球,其中1个红色球,3个黄色球.
(1)从口袋中随机取出一个球(不放回),接着再取出一个球,请用树形图或列表的方法求取出的两个球一个是红色球,一个是黄色球的概率;
(2)小明往该口袋中又放入m个红色球和(m+2)个黄色球,再从口袋中随机取出一个球,这个球是黄色球的概率为![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=2x+2分别与x轴,y轴交于点A、B,已知点A1是点A关于y轴的对称点,作直线A1B,过点A1作x轴的垂线l1,交直线AB于点B1;点A2是点A关于直线l1的对称点,作直线A2B1,过点A2作x轴的垂线l2,交直线AB于B2;点A3是点A关于l2的对称点,作直线A3B2……继续这样操作下去,可作直线AnBn﹣1.(n为正整数,且n≥1)
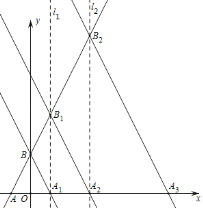
(1)填空:
①A1(1,0),A2(3,0),A3( , ),An( , );
②B(0,2),B1(1,4),B2( , ),Bn﹣1( , );
(2)求线段AnBn﹣1的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com