
【题目】如图,抛物线![]() 与x轴交于A,B,与y轴交于点C(0,2),直线
与x轴交于A,B,与y轴交于点C(0,2),直线![]() 经过点A,C.
经过点A,C.
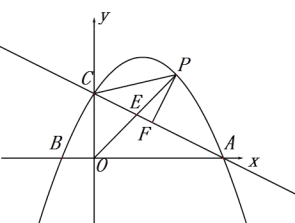
(1)求抛物线的解析式;
(2)点P为直线AC上方抛物线上一动点;
①连接PO,交AC于点E,求![]() 的最大值;
的最大值;
②过点P作PF⊥AC,垂足为点F,连接PC,是否存在点P,使△PFC中的一个角等于∠CAB的2倍?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() 有最大值1;②(2,3)或(
有最大值1;②(2,3)或(![]() ,
,![]() )
)
【解析】
(1)根据自变量与函数值的对应关系,可得A,C点坐标,根据代定系数法,可得函数解析式;
(2)①根据相似三角形的判定与性质,可得![]() ,根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可得答案;
,根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可得答案;
②根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形,取AB的中点D,求得D(![]() ,0),得到DA=DC=DB=
,0),得到DA=DC=DB=![]() ,过P作x轴的平行线交y轴于R,交AC于G,情况一:如图,∠PCF=2∠BAC=∠DGC+∠CDG,情况二,∠FPC=2∠BAC,解直角三角形即可得到结论.
,过P作x轴的平行线交y轴于R,交AC于G,情况一:如图,∠PCF=2∠BAC=∠DGC+∠CDG,情况二,∠FPC=2∠BAC,解直角三角形即可得到结论.
(1)当x=0时,y=2,即C(0,2),
当y=0时,x=4,即A(4,0),
将A,C点坐标代入函数解析式,得
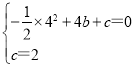 ,
,
解得![]() ,
,
抛物线的解析是为![]() ;
;
(2)过点P向x轴做垂线,交直线AC于点M,交x轴于点N
 ,
,
∵直线PN∥y轴,
∴△PEM~△OEC,
∴![]()
把x=0代入y=-![]() x+2,得y=2,即OC=2,
x+2,得y=2,即OC=2,
设点P(x,-![]() x2+
x2+![]() x+2),则点M(x,-
x+2),则点M(x,-![]() x+2),
x+2),
∴PM=(-![]() x2+
x2+![]() x+2)-(-
x+2)-(-![]() x+2)=-
x+2)=-![]() x2+2x=-
x2+2x=-![]() (x-2)2+2,
(x-2)2+2,
∴![]() =
= ,
,
∵0<x<4,∴当x=2时,![]() =
= 有最大值1.
有最大值1.
②∵A(4,0),B(-1,0),C(0,2),
∴AC=2![]() ,BC=
,BC=![]() ,AB=5,
,AB=5,
∴AC2+BC2=AB2,
∴△ABC是以∠ACB为直角的直角三角形,取AB的中点D,
∴D(![]() ,0),
,0),
∴DA=DC=DB=![]() ,
,
∴∠CDO=2∠BAC,
∴tan∠CDO=tan(2∠BAC)=![]() ,
,
过P作x轴的平行线交y轴于R,交AC的延长线于G,
情况一:如图
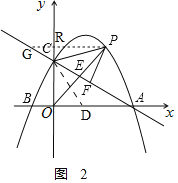 ,
,
∴∠PCF=2∠BAC=∠PGC+∠CPG,
∴∠CPG=∠BAC,
∴tan∠CPG=tan∠BAC=![]() ,
,
即![]() ,
,
令P(a,-![]() a2+
a2+![]() a+2),
a+2),
∴PR=a,RC=-![]() a2+
a2+![]() a,
a,
∴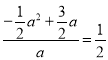 ,
,
∴a1=0(舍去),a2=2,
∴xP=2,-![]() a2+
a2+![]() a+2=3,P(2,3)
a+2=3,P(2,3)
情况二,∴∠FPC=2∠BAC,
∴tan∠FPC=![]() ,
,
设FC=4k,
∴PF=3k,PC=5k,
∵tan∠PGC=![]() ,
,
∴FG=6k,
∴CG=2k,PG=3![]() k,
k,
∴RC=![]() k,RG=
k,RG=![]() k,PR=3
k,PR=3![]() k-
k-![]() k=
k=![]() k,
k,
∴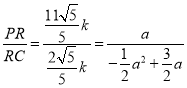 ,
,
∴a1=0(舍去),a2=![]() ,
,
xP=![]() ,-
,-![]() a2+
a2+![]() a+2=
a+2=![]() ,即P(
,即P(![]() ,
,![]() ),
),
综上所述:P点坐标是(2,3)或(![]() ,
,![]() ).
).


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,∠ABC=72°,过点A作BC的平行线与∠ABC的平分线交于点D,BD交AC于点E,交⊙O于点F,连接AF.
(1)求证:AD是⊙O的切线;
(2)已知BC=2,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF.
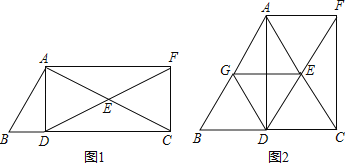
(1)如图1,求证:四边形ADCF是矩形;
(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在一个不透明的口袋中有4个形状、大小、材质完全相同的球,其中1个红色球,3个黄色球.
(1)从口袋中随机取出一个球(不放回),接着再取出一个球,请用树形图或列表的方法求取出的两个球一个是红色球,一个是黄色球的概率;
(2)小明往该口袋中又放入m个红色球和(m+2)个黄色球,再从口袋中随机取出一个球,这个球是黄色球的概率为![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,直线y=kx+b交BC于点E(1,m),交AB于点F(4,![]() ),反比例函数y=
),反比例函数y=![]() (x>0)的图象经过点E,F.
(x>0)的图象经过点E,F.
(1)求反比例函数及一次函数解析式;
(2)点P是线段EF上一点,连接PO、PA,若△POA的面积等于△EBF的面积,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
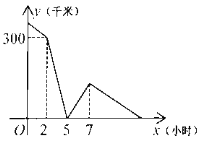
【题目】甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发两小时,甲车到达B地后立即调头,并保持原速度与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶,经过一段时间后两车同时到达C地,设两车之间的距离为y(干米),甲车行驶的时间为x小时,y与x之间的函数图象如图所示,则当甲车重返A地时,乙车距离C地________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3).反比例函数y=![]() (x>0)的图像经过点D,P是一次函数y=kx+3-3k(k≠0)的图像与该反比例函数图像的一个公共点.
(x>0)的图像经过点D,P是一次函数y=kx+3-3k(k≠0)的图像与该反比例函数图像的一个公共点.
(1)求反比例函数的表达式;
(2)通过计算说明一次函数y=kx+3-3k(k≠0)的图像一定经过点C;
(3)对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围(不必写出过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=2x+2分别与x轴,y轴交于点A、B,已知点A1是点A关于y轴的对称点,作直线A1B,过点A1作x轴的垂线l1,交直线AB于点B1;点A2是点A关于直线l1的对称点,作直线A2B1,过点A2作x轴的垂线l2,交直线AB于B2;点A3是点A关于l2的对称点,作直线A3B2……继续这样操作下去,可作直线AnBn﹣1.(n为正整数,且n≥1)
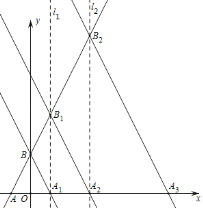
(1)填空:
①A1(1,0),A2(3,0),A3( , ),An( , );
②B(0,2),B1(1,4),B2( , ),Bn﹣1( , );
(2)求线段AnBn﹣1的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍,为了了解学生的选择意向,随机抽取A,B,C,D四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图(不完整)
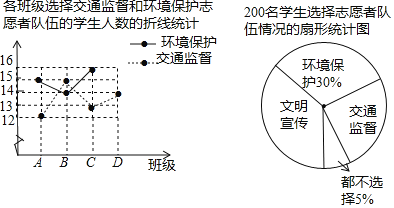
(1)求扇形统计图中交通监督所在扇形的圆心角度数;
(2)求D班选择环境保护的学生人数,并补全折线统计图;(温馨提示:请画在答题卷相对应的图上)
(3)若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com