
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,直线y=kx+b交BC于点E(1,m),交AB于点F(4,![]() ),反比例函数y=
),反比例函数y=![]() (x>0)的图象经过点E,F.
(x>0)的图象经过点E,F.
(1)求反比例函数及一次函数解析式;
(2)点P是线段EF上一点,连接PO、PA,若△POA的面积等于△EBF的面积,求点P的坐标.

【答案】(1)![]() ;
;![]() ;(2)点P坐标为(
;(2)点P坐标为(![]() ,
,![]() ).
).
【解析】
(1)将F(4,![]() )代入
)代入![]() ,即可求出反比例函数的解析式
,即可求出反比例函数的解析式![]() ;再根据
;再根据![]() 求出E点坐标,将E、F两点坐标代入
求出E点坐标,将E、F两点坐标代入![]() ,即可求出一次函数解析式;
,即可求出一次函数解析式;
(2)先求出△EBF的面积,
点P是线段EF上一点,可设点P坐标为![]() ,
,
根据面积公式即可求出P点坐标.
解:(1)∵反比例函数![]() 经过点
经过点![]() ,
,
∴n=2,
反比例函数解析式为![]() .
.
∵![]() 的图象经过点E(1,m),
的图象经过点E(1,m),
∴m=2,点E坐标为(1,2).
∵直线![]() 过点
过点![]() ,点
,点![]() ,
,
∴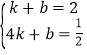 ,解得
,解得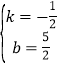 ,
,
∴一次函数解析式为![]() ;
;
(2)∵点E坐标为(1,2),点F坐标为![]() ,
,
∴点B坐标为(4,2),
∴BE=3,BF=![]() ,
,
∴![]() ,
,
∴![]() .
.
点P是线段EF上一点,可设点P坐标为![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴点P坐标为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当ΔCB′E为直角三角形时,则AE的长为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 延长线上一点,过点
延长线上一点,过点![]() 作
作![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连结
,连结![]() 、
、![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,试判断四边形
,试判断四边形![]() 是什么样的四边形,并证明你的结论;
是什么样的四边形,并证明你的结论;
![]() 若
若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给的网格图中,完成下列各题(用直尺画图,否则不给分)
(1)画出格点△ABC关于直线DE的对称的△A1B1C1;
(2)在DE上画出点P,使PA+PC最小;
(3)在DE上画出点Q,使QA﹣QB最大.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察与发现:小明将三角形纸片![]() 沿过点
沿过点![]() 的直线折叠,使得
的直线折叠,使得![]() 落在
落在![]() 边上,折痕为
边上,折痕为![]() ,展开纸片(如图①);在第一次的折叠基础上第二次折叠该三角形纸片,使点
,展开纸片(如图①);在第一次的折叠基础上第二次折叠该三角形纸片,使点![]() 和点
和点![]() 重合,折痕为
重合,折痕为![]() ,展平纸片后得到
,展平纸片后得到![]() (如图②).小明认为
(如图②).小明认为![]() 是等腰三角形,你同意吗?请说明理由.
是等腰三角形,你同意吗?请说明理由.
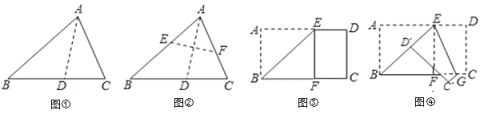
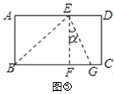
(2)实践与运用:将矩形纸片![]() 沿过点
沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() (如图③);再沿过点
(如图③);再沿过点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() (如图④);再展平纸片(如图⑤).求图⑤中
(如图④);再展平纸片(如图⑤).求图⑤中![]() 的大小。
的大小。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图1中的矩形ABCD沿对角线AC剪开,再把△ABC沿着AD方向平移,得到图2中的△A′BC′.
(1)在图2中,除△ADC与△C′BA′全等外,请写出其他2组全等三角形;① ;② ;
(2)请选择(1)中的一组全等三角形加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com