
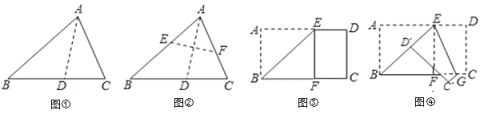
����Ŀ��(1)�۲��뷢�֣�С����������ֽƬ![]() �ع���
�ع���![]() ��ֱ���۵�,ʹ��
��ֱ���۵�,ʹ��![]() ����
����![]() ����,�ۺ�Ϊ
����,�ۺ�Ϊ![]() ,չ��ֽƬ(��ͼ��);�ڵ�һ�ε��۵������ϵڶ����۵���������ֽƬ,ʹ��
,չ��ֽƬ(��ͼ��);�ڵ�һ�ε��۵������ϵڶ����۵���������ֽƬ,ʹ��![]() �͵�
�͵�![]() �غ�,�ۺ�Ϊ
�غ�,�ۺ�Ϊ![]() ,չƽֽƬ��õ�
,չƽֽƬ��õ�![]() (��ͼ��).С����Ϊ
(��ͼ��).С����Ϊ![]() �ǵ��������Σ���ͬ����?��˵������.
�ǵ��������Σ���ͬ����?��˵������.
(2)ʵ�������ã�������ֽƬ![]() �ع���
�ع���![]() ��ֱ���۵�,ʹ��
��ֱ���۵�,ʹ��![]() ����
����![]() ���ϵĵ�
���ϵĵ�![]() ��,�ۺ�Ϊ
��,�ۺ�Ϊ![]() (��ͼ��);���ع���
(��ͼ��);���ع���![]() ��ֱ���۵�,ʹ��
��ֱ���۵�,ʹ��![]() ����
����![]() �ϵĵ�
�ϵĵ�![]() ��,�ۺ�Ϊ
��,�ۺ�Ϊ![]() (��ͼ��);��չƽֽƬ(��ͼ��).��ͼ����
(��ͼ��);��չƽֽƬ(��ͼ��).��ͼ����![]() �Ĵ�С��
�Ĵ�С��
���𰸡�(1)ͬ��.���ɼ�������(2) ![]() .
.
��������
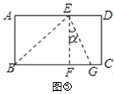
��1���������۵�֪����A��EF���д����ϣ�����AE=AF��
��2����ͼ֪������=��FED����180�㩁��AEB����2��
��1��ͬ�⣮��ͼ����AD��EF���ڵ�G��
���۵�֪��ADƽ�֡�BAC�����ԡ�BAD=��CAD��
�����۵�֪����AGE=��DGE����AGE+��DGE=180�㣬
���ԡ�AGE=��AGF=90�㣬
���ԡ�AEF=��AFE������AE=AF��
����AEF����������
��2�����۵�֪���ı���ABFE�������Σ���AEB=45�㣬
���ԡ�BED=135�ȣ�
�����۵�֪����BEG=��DEG��
���ԡ�DEG=67.5�ȣ�
�Ӷ�����=67.5�㩁45��=22.5�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() �У�
��![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �ӳ����ϵ�һ�㣬
�ӳ����ϵ�һ�㣬![]() �ӳ���
�ӳ���![]() ��
��![]() ��
��![]() ��С���ó�
��С���ó�![]() �����ۣ���
�����ۣ���![]() ����
����![]() ����
����![]() ��
��
������ȷ���ǣ� ��

A. �٢� B. �٢� C. �ڢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����M��N�ֱ���������ABCD�ı�BC��CD�ϵĵ㣬��BM��CN�� AM��BN���ڵ�P����̽��AM��BN�Ĺ�ϵ.
��1��������ϵ_____________________����֤����
��2��λ�ù�ϵ_____________________����֤��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
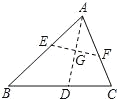
����Ŀ����ͼ����PΪ������AOB��ƽ�����ϵ�һ�����㣬����MPN����AOB����������MPN���Ƶ�P��ת�Ĺ����У������߷ֱ���OA��OB�ཻ��M��N���㣬�����½��ۣ���1��PM=PN���������2��OM+ON��ֵ���䣻��3���ı���PMON��������䣻��4��MN�ij����䣬������ȷ�ĸ���Ϊ��������

A. 4B. 3C. 2D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���OABCΪ���Σ�ֱ��y=kx+b��BC�ڵ�E��1��m������AB�ڵ�F��4��![]() ��������������y=
��������������y=![]() ��x��0����ͼ����E��F��
��x��0����ͼ����E��F��
��1������������һ�κ�������ʽ��
��2����P���߶�EF��һ�㣬����PO��PA������POA��������ڡ�EBF����������P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����y=x+1��ͼ����y�ύ�ڵ�A��һ�κ���y=kx+b��ͼ����B��0����1������x���Լ�y=x+1��ͼ��ֱ��ڵ�C��D���ҵ�D������Ϊ��1��n����
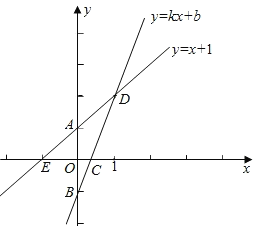
��1����һ�κ���y=kx+b�ĺ�����ϵʽ
��2�����ı���AOCD�������
��3���Ƿ����y���ϵĵ�P��ʹ����BDΪ�ġ�PBD���������Σ������������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y=ax+b�����ڶ������������ޣ���ô���н�����ȷ���ǣ�������
A. ![]() =a+b
=a+b
B. �㣨a��b���ڵ�һ������
C. ����������![]() ����x��0ʱ������ֵy��x�������С
����x��0ʱ������ֵy��x�������С
D. ������y=ax2+bx+c�ĶԳ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���1����600Ԫ����2BǦ������֧����2����800Ԫ�ֹ����ÿ�Ǧ�ʣ������ÿ֧�Ľ����ǵ�1�ν��۵İ��ۣ��ҹ��������ȵ�1�ζ���100֧��
��1�����1��ÿ֧2BǦ�ʵĽ��ۣ�
��2����Ҫ�������ι�����2BǦ�ʰ�ͬһ�۸�ȫ��������Ϻ����������600Ԫ����ÿ֧2BǦ�ʵ��ۼ������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ĵױ�BC��Ϊ4�������16����AC�Ĵ�ֱƽ����EF�ֱ�AC��AB����E��F�㣬����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬��![]() �ܳ�����СֵΪ______��
�ܳ�����СֵΪ______��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com