
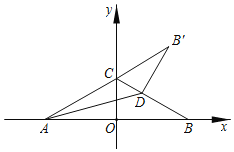
【题目】如图,直线y=![]() x+1分别交x轴、y轴于点A、C,点B是点A关于y的对称点,点D是线段BC上一点,把△ABD沿AD翻折使AB落在射线AC上,得△AB'D,则△ABC与△AB'D重叠部分的面积为( )
x+1分别交x轴、y轴于点A、C,点B是点A关于y的对称点,点D是线段BC上一点,把△ABD沿AD翻折使AB落在射线AC上,得△AB'D,则△ABC与△AB'D重叠部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
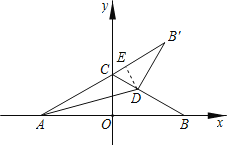
首先过点D作DE⊥AB′于点E,由直线的解析式和轴对称的性质求得∠CAB=∠B=30°,AB=2![]() ,利用勾股定理即可求得AC的长,又由折叠的性质,易得∠CDB′=90°,∠B′=30°,B′C=AB′﹣AC=2
,利用勾股定理即可求得AC的长,又由折叠的性质,易得∠CDB′=90°,∠B′=30°,B′C=AB′﹣AC=2![]() ﹣2,继而求得CD与B′D的长,然后求得高DE的长,继而求得答案.
﹣2,继而求得CD与B′D的长,然后求得高DE的长,继而求得答案.
解:过点D作DE⊥AB′于点E,
∵直线y=![]() x+1分别交x轴、y轴于点A、C,
x+1分别交x轴、y轴于点A、C,
∴OA=![]() ,OC=1,∠OAC=30°,
,OC=1,∠OAC=30°,
∴AC=![]() =2,
=2,
∵点B是点A关于y的对称点,
∴OA=OB=![]() ,AC=BC=2,
,AC=BC=2,
∴AB=2![]() ,∠OBC=∠OAC=30°,
,∠OBC=∠OAC=30°,
由折叠的性质得:AB′=AB=2![]() ,∠B′=∠ABC=30°,
,∠B′=∠ABC=30°,
∵∠B′CD=∠CAB+∠ABC=60°,
∴∠CDB′=90°,
∵B′C=AB′﹣AC=2![]() ﹣2,
﹣2,
∴CD=![]() B′C=
B′C=![]() ﹣1,B′D=B′Ccos∠B′=(2
﹣1,B′D=B′Ccos∠B′=(2![]() ﹣2)×
﹣2)×![]() =3﹣
=3﹣![]() ,
,
∴DE=![]() =
=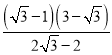 =
=![]() ,
,
∴S重叠=![]() ACDE=
ACDE=![]() ×2×
×2×![]() =
=![]() .
.
故选:A.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】我国为了实现到2020年达到全面小康社会的目标,近几年加大了扶贫工作的力度,合肥市某知名企业为了帮助某小型企业脱贫,投产一种书包,每个书包制造成本为18元,试销过程中发现,每月销售量y(万个)与销售单价x(元)之间的关系可以近似看作一次函数y=kx+b,据统计当售价定为30元/个时,每月销售40万个,当售价定为35元/个时,每月销售30万个.
(1)请求出k、b的值.
(2)写出每月的利润w(万元)与销售单价x(元)之间的函数解析式.
(3)该小型企业在经营中,每月销售单价始终保持在25≤x≤36元之间,求该小型企业每月获得利润w(万元)的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD是半圆O的直径,A是BD延长线上的一点,BC⊥AE,交AE的延长线于点C,交半圆O于点E,且E为![]() 的中点.
的中点.
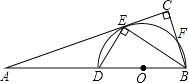
(1)求证:AC是半圆O的切线;
(2)若AD=6,AE=6![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的函数,自变量
的函数,自变量![]() 的取值范围是
的取值范围是![]() 的全体实数,如表是
的全体实数,如表是![]() 与
与![]() 的几组对应值.
的几组对应值.

小华根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
之间的变化规律,对该函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)从表格中读出,当自变量是﹣2时,函数值是 ;
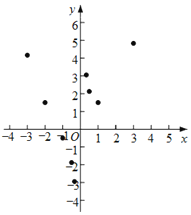
(2)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(3)在画出的函数图象上标出![]() 时所对应的点,并写出
时所对应的点,并写出![]() .
.
(4)结合函数的图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,∠ABC=72°,过点A作BC的平行线与∠ABC的平分线交于点D,BD交AC于点E,交⊙O于点F,连接AF.
(1)求证:AD是⊙O的切线;
(2)已知BC=2,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
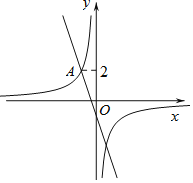
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
![]() 求双曲线
求双曲线![]() 的表达式;
的表达式;
![]() 过动点
过动点![]() 且垂直于x轴的直线与直线
且垂直于x轴的直线与直线![]() 及双曲线
及双曲线![]() 的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年农历五月初五为端午节,中国民间历来有端午节吃粽子、赛龙舟的习俗.某班同学为了更好地了解某社区居民对鲜肉粽(A)豆沙粽(B)小枣粽(C)蛋黄粽(D)的喜爱情况,对该社区居民进行了随机抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

分析图中信息,本次抽样调查中喜爱小枣粽的人数为________;若该社区有10000人,估计爱吃鲜肉粽的人数约为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,直线y=kx+b交BC于点E(1,m),交AB于点F(4,![]() ),反比例函数y=
),反比例函数y=![]() (x>0)的图象经过点E,F.
(x>0)的图象经过点E,F.
(1)求反比例函数及一次函数解析式;
(2)点P是线段EF上一点,连接PO、PA,若△POA的面积等于△EBF的面积,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com