
【题目】如图,△ABC是定圆O的内接三角形,AD为△ABC的高线,AE平分∠BAC交⊙O于E,交BC于G,连OE交BC于F,连OA,在下列结论中,①CE=2EF,②△ABG∽△AEC,③∠BAO=∠DAC,④ ![]() 为常量.其中正确的有 .
为常量.其中正确的有 . 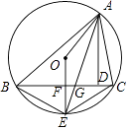
【答案】②,③,④
【解析】解:∵∠BCE的度数不一定为30°, ∴Rt△CEF中,CE=2EF不一定成立,故①错误;
∵AE平分∠BAC,
∴∠BAG=∠EAC,
又∵∠ABG=∠AEC,
∴△ABG∽△AEC,故②正确;
如图所示,延长AO交⊙O于点H,连接BH,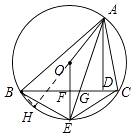
∵AH是⊙O直径,AD⊥BC,
∴∠ABH=90°,∠ADC=90°,
∴∠H+∠BAH=90°,∠C+∠ACD=90°,
∵∠H=∠ACD,
∴∠BAH=∠DAC,故③正确;
∵∠BAH=∠DAC,∠ABH=∠ADC,
∴△ABH∽△ADC,
∴ ![]() =
= ![]() ,即AH=
,即AH= ![]() ,
,
又∵AH为常量,
∴ ![]() 为常量,故④正确;
为常量,故④正确;
故答案为:②,③,④.
根据圆周角定理以及相似三角形的判定方法,即可得出△ABG∽△AEC,△ABH∽△ADC,再根据相似三角形的对应边成比例即可得出结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2 , 如此继续下去,则正六边形A4B4C4D4E4F4的面积是. 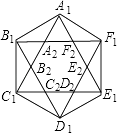
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 都是边长为1的等边三角形.
都是边长为1的等边三角形.
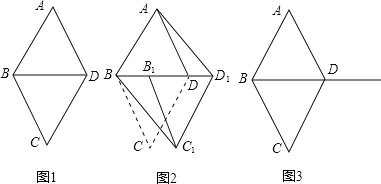
![]() 四边形ABCD是菱形吗?为什么?
四边形ABCD是菱形吗?为什么?
![]() 如图2,将
如图2,将![]() 沿射线BD方向平移到
沿射线BD方向平移到![]() 的位置,则四边形
的位置,则四边形![]() 是平行四边形吗?为什么?
是平行四边形吗?为什么?
![]() 在
在![]() 移动过程中,四边形
移动过程中,四边形![]() 有可能是矩形吗?如果是,请求出点B移动的距离
有可能是矩形吗?如果是,请求出点B移动的距离![]() 写出过程
写出过程![]() ;如果不是,请说明理由
;如果不是,请说明理由![]() 图3供操作时使用
图3供操作时使用![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.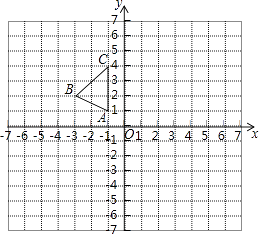
①画出与△ABC关于y轴对称的△A1B1C1 , 求点C1的坐标。
②以原点O为位似中心,在第四象限画一个△A2B2C2 , 使它与△ABC位似,并且△A2B2C2与△ABC的相似比为2:1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,点A、B在x轴上,AB⊥BC,AO=OB=2,BC=3
(1)写出点A、B、C的坐标.
(2)如图②,过点B作BD∥AC交y轴于点D,求∠CAB+∠BDO的大小.
(3)如图③,在图②中,作AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠BOC、∠BOF的度数.
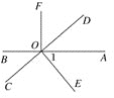
解:∵OE⊥CD( ),
∴∠DOE=_____°( ),
∵∠1=50°( ),
∴∠AOD=∠________-∠________=________°,
∵∠BOC与∠AOD为_______角(____________),
∴∠BOC=∠________=∠_________°(_____________),
∵OD平分∠AOF(______________),
且∠AOD=____________°(______________),
∴∠AOF=2∠__________=________°( ),
∵∠BOF+∠AOF=______°( ),
∴∠BOF=______°-∠AOF=_________°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com