
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
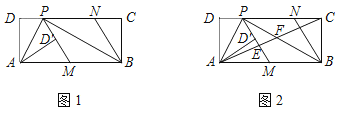
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC分别交PM、PB于点E、F.若AD=3DP,探究EF与AE之间的的数量关系.
【答案】(1)见解析;(2)四边形PMBN是菱形;理由见解析;(3)![]() .
.
【解析】
(1)过点P作PG⊥AB于点G,易知四边形DPGA,四边形PCBG是矩形,所以AD=PG,DP=AG,GB=PC,易证△APG∽△PBG,所以PG2=AGGB,即AD2=DPPC;
(2)DP∥AB,所以∠DPA=∠PAM,由题意可知:∠DPA=∠APM,所以∠PAM=∠APM,由于∠APB∠PAM=∠APB∠APM,即∠ABP=∠MPB,从而可知PM=MB=AM,又易证四边形PMBN是平行四边形,所以四边形PMBN是菱形;
(3)由于AD=3DP,可设设DP=1,则AD=3,由(1)可知:AG=DP=1,PG=AD=3,从而求出BG=PC=9,AB=AG+BG=10,由于CP∥AB,从而可证△PCF∽△BAF,△PCE∽△MAE,从而可得![]() =
=![]() ,
,![]() =
=![]() ,从而可求出EF=AF﹣AE=
,从而可求出EF=AF﹣AE=![]() AC﹣
AC﹣![]() AC=
AC=![]() AC,从而可得
AC,从而可得![]() =
= =
=![]() .
.
(1)证明:过点P作PG⊥AB于点G,如图1所示:

则四边形DPGA和四边形PCBG是矩形,
∴AD=PG,DP=AG,BG=PC,
∵∠APB=90°,
∴∠APG+∠GPB=∠GPB+∠PBG=90°,
∴∠APG=∠PBG,
∴△APG∽△PBG,
∴![]() =
=![]() ,
,
∴PG2=AGBG,
即AD2=DPPC;
(2)解:四边形PMBN是菱形;理由如下:
∵四边形ABCD是矩形,
∴AB∥CD,
∵BM∥PN,BN∥MP,
∴四边形PMBN是平行四边形,
∵DP∥AB,
∴∠DPA=∠PAM,
由题意可知:∠DPA=∠APM,
∴∠PAM=∠APM,
∵∠APB﹣∠PAM=∠APB﹣∠APM,
即∠ABP=∠MPB
∴AM=PM,PM=MB,
∴PM=MB,
∴四边形PMBN是菱形;
(3)解:∵AD=3DP,
∴设DP=1,则AD=3,
由(1)可知:AG=DP=1,PG=AD=3,
∵PG2=AGBG,
∴32=1BG,
∴BG=PC=9,
AB=AG+BG=10,
∵CP∥AB,
∴△PCF∽△BAF,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵PM=MB,
∴∠MPB=∠MBP,
∵∠APB=90°,
∴∠MPB+∠APM=∠MBP+∠MAP=90°,
∴∠APM=∠MAP,
∴PM=MA=MB,
∴AM=![]() AB=5,
AB=5,
∵AB∥CD,
∴△PCE∽△MAE,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴EF=AF﹣AE=![]() AC﹣
AC﹣![]() AC=
AC=![]() AC,
AC,
∴![]() =
= =
=


科目:初中数学 来源: 题型:
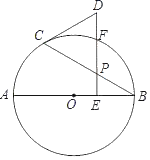
【题目】如图,已知AB是⊙O的直径,点P是弦BC上一动点(不与端点重合),过点P作PE⊥AB于点E,延长EP交![]() 于点F,交过点C的切线于点D.
于点F,交过点C的切线于点D.
(1)求证:△DCP是等腰三角形;
(2)若OA=6,∠CBA=30°.
①当OE=EB时,求DC的长;
②当![]() 的长为多少时,以点B,O,C,F为顶点的四边形是菱形?
的长为多少时,以点B,O,C,F为顶点的四边形是菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x﹣3.

(1)将二次函数y=x2+2x﹣3化成顶点式.
(2)求图象与x轴,y轴的交点坐标.
(3)在坐标系中利用描点法画出此抛物线.
(4)当x取何值时,y随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
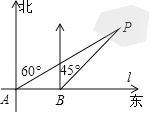
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
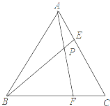
【题目】如图,等边三角形ABC的边长为![]() cm,在AC,BC边上各取一点E,F,使得AE=CF,连接AF,BE相交于点P.(1)则∠APB=______度;(2)当点E从点A运动到点C时,则动点P经过的路径长为________cm.
cm,在AC,BC边上各取一点E,F,使得AE=CF,连接AF,BE相交于点P.(1)则∠APB=______度;(2)当点E从点A运动到点C时,则动点P经过的路径长为________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是一款手机支架,忽略支管的粗细,得到它的简化结构图如图(2)所示.已知支架底部支架CD平行于水平面,EF⊥OE,GF⊥EF,支架可绕点O旋转,OE=20cm,EF=20![]() cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
cm.如图(3)若将支架上部绕O点逆时针旋转,当点G落在直线CD上时,测量得∠EOG=65°.
(1)求FG的长度(结果精确到0.1);
(2)将支架由图(3)转到图(4)的位置,若此时F、O两点所在的直线恰好于CD垂直,点F的运动路线的长度称为点F的路径长,求点F的路径长.
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连结AC、OC、BC.
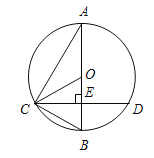
(1)求证:∠ACO=∠BCD;
(2)若EB=2cm,CD=8m,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区有一长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为( )米.
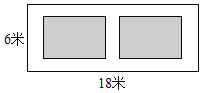
A. 2B. 1C. 8或1D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com