
【题目】下表中给出![]() ,
,![]() ,
,![]() 三种手机通话的收费方式.
三种手机通话的收费方式.
收费方式 | 月通话费/元 | 包时通话时间/ | 超时费/(元/ |
|
|
|
|
|
|
|
|
|
| 不限时 |
(1)设月通话时间为![]() 小时,则方案
小时,则方案![]() ,
,![]() ,
,![]() 的收费金额
的收费金额![]() ,
,![]() ,
,![]() 都是
都是![]() 的函数,请分别求出这三个函数解析式.
的函数,请分别求出这三个函数解析式.
(2)填空:
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
(3)小王、小张今年![]() 月份通话费均为
月份通话费均为![]() 元,但小王比小张通话时间长,求小王该月的通话时间.
元,但小王比小张通话时间长,求小王该月的通话时间.
【答案】(1)![]() (2)
(2) ![]() (3)
(3)![]()
【解析】
(1)根据题意可以分别写出![]() 、
、![]() 、
、![]() 关于
关于![]() 的函数关系式,并写出相应的自变量的取值范围;
的函数关系式,并写出相应的自变量的取值范围;
(2)根据题意作出图象,结合图象即可作答;
(3)结合图象可得:小张选择的是方式![]() ,小王选择的是方式
,小王选择的是方式![]() ,将
,将![]() 代入
代入![]() 关于
关于![]() 的函数关系式,解方程即可得出小王该月的通话时间.
的函数关系式,解方程即可得出小王该月的通话时间.
(1)∵0.1元/![]() 元/
元/![]() ,
,
![]() 由题意可得,
由题意可得,
![]() ,
,
![]() ,
,
![]() ;
;
(2)作出函数图象如图:
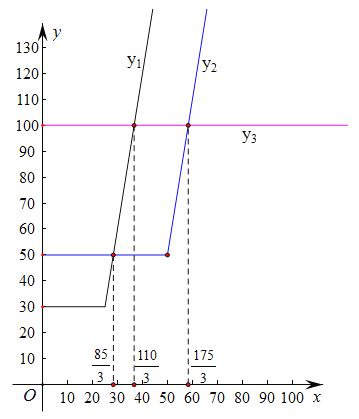
结合图象可得:
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为:
的取值范围为:![]() ,
,
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为:
的取值范围为:![]() ,
,
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为:
的取值范围为:![]() .
.
故答案为:![]() ,
,![]() ,
,![]() .
.
(3)∵小王、小张今年![]() 月份通话费均为
月份通话费均为![]() 元,但小王比小张通话时间长,
元,但小王比小张通话时间长,
![]() 结合图象可得:小张选择的是方式
结合图象可得:小张选择的是方式![]() ,小王选择的是方式
,小王选择的是方式![]() ,
,
将![]() 分别代入
分别代入![]() ,可得
,可得
![]() ,
,
解得:![]() ,
,
![]() 小王该月的通话时间为
小王该月的通话时间为![]() 小时.
小时.


科目:初中数学 来源: 题型:
【题目】已知直线x=1是二次函数y=ax2+bx+c(a,b,c是实数,且a≠0)的图象的对称轴,点A(x1,y1)和点B(x2,y2)为其图象上的两点,且y1<y2,( )
A.若x1<x2,则x1+x2﹣2<0B.若x1<x2,则x1+x2﹣2>0
C.若x1>x2,则a(x1+x2-2)>0D.若x1>x2,则a(x1+x2-2)<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图所示.
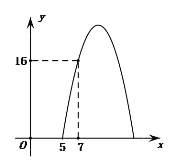
⑴a= ;b= ;
⑵销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
⑶由图象可知,销售单价x在 时,该种商品每天的销售利润不低于16元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日是世界读书日,设立的目的是推动更多的人去阅读和写作.为了解学生的课外阅读情况,对某校八年级1班“你最喜爱的课外阅读书目”进行调查(每名学生必须选一类且只能选一类阅读书目),并根据调查结果绘制成如图所示的两幅统计图(不完整).
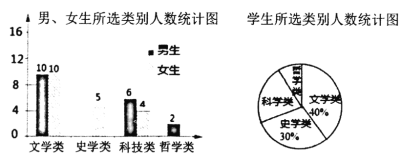
根据以上信息解决下列问题
(1)所抽查的学生中,选史学类的男生有______人,选哲学类的女生有______人;
(2)扇形统计图中“科学类”所对应扇形圆心角度数为_______°;
(3)若该校有2000名学生,请估计该校喜爱“科学类”的学生共有多少人?
(4)从所抽取的选“哲学类”的学生中,随机选取两名学生参加区级辩论赛,请用树状图或列表法求出所选取的两名学生恰好选中一个男生、一个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,对称轴为直线
,对称轴为直线![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的一个根.其中正确的有( )
的一个根.其中正确的有( )
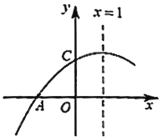
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
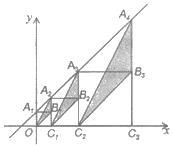
【题目】在直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,按如图方式作正方形
,按如图方式作正方形![]() 、
、![]() 、
、![]() ,点
,点![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 、
、![]() 在
在![]() 轴上,图中阴影部分三角形的面积从左到右依次记为
轴上,图中阴影部分三角形的面积从左到右依次记为![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论: ①方程x2+2x﹣8=0是倍根方程;
②若关于x的方程x2+ax+2=0是倍根方程,则a=±3;
③若关于x的方程ax2﹣6ax+c=0(a≠0)是倍根方程,则抛物线y=ax2﹣6ax+c与x轴的公共点的坐标是(2,0)和(4,0);
④若点(m,n)在反比例函数y=![]() 的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
的图象上,则关于x的方程mx2+5x+n=0是倍根方程.
上述结论中正确的有( )
A. ①② B. ③④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
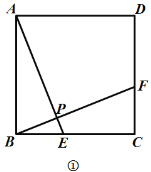
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图①,判断![]() 和
和![]() 之间的数量关系和位置关系,并证明;
之间的数量关系和位置关系,并证明;
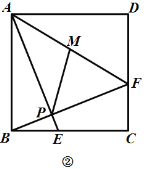
(2)如图②,连接![]() ,点
,点![]() 是
是![]() 中点,若
中点,若![]() ,
,![]() ,求线段
,求线段![]() 的长度;
的长度;
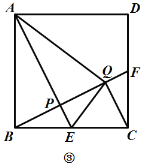
(3)如图③,作![]() 于点
于点![]() ,若
,若![]() ,求证:点
,求证:点![]() 是
是![]() 中点.
中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于两个点
中,对于两个点![]() ,
,![]() 和图形
和图形![]() ,如果在图形上存在点
,如果在图形上存在点![]() ,
,![]() (
(![]() ,
,![]() 可以重合),使得
可以重合),使得![]() ,那么称点
,那么称点![]() 与点
与点![]() 是图形
是图形![]() 的一对“倍点”.已知⊙O的半径为
的一对“倍点”.已知⊙O的半径为![]() ,点
,点![]() .
.
(1)①点![]() 到⊙O的最大值是_______,最小值是_______;
到⊙O的最大值是_______,最小值是_______;
②在![]() ,
,![]() ,这两个点中,与点
,这两个点中,与点![]() 是⊙O的一对“倍点”的是_______;
是⊙O的一对“倍点”的是_______;
(2)在直线![]() 上存在点
上存在点![]() 与点
与点![]() 是⊙O的一对“倍点”,求
是⊙O的一对“倍点”,求![]() 的取值范围;
的取值范围;
(3)已知直线![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点的
轴分别交于点的![]() ,
,![]() ,若线段
,若线段![]() (含端点
(含端点![]() ,
,![]() )上所有点与点
)上所有点与点![]() 都是⊙O的一对“倍点”,直接写出
都是⊙O的一对“倍点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com