
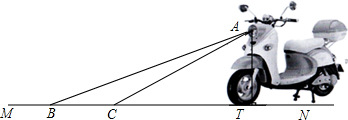
分析 (1)在直角△ACT中,根据三角函数的定义,若AT=3x,则CT=5x,在直角△ABT中利用三角函数即可列方程求解;
(2)求出正常人作出反应过程中电动车行驶的路程,加上刹车距离,然后与BT的长进行比较即可.
解答 解:(1)根据题意及图知:∠ACT=31°,∠ABT=22°
∵AT⊥MN
∴∠ATC=90°
在Rt△ACT中,∠ACT=31°
∴tan31°=$\frac{AT}{CT}=\frac{3}{5}$
可设AT=3x,则CT=5x
在Rt△ABT中,∠ABT=22°
∴tan22°=$\frac{AT}{BT}=\frac{AT}{BC+CT}=\frac{2}{5}$
即:$\frac{3x}{{\frac{5}{6}+5x}}=\frac{2}{5}$
解得:$x=\frac{1}{3}$
∴$CT=5×\frac{1}{3}=\frac{5}{3}$,
∴$BT=BC+CT=\frac{5}{6}+\frac{5}{3}=\frac{5}{2}m$;
(2)$20km/h=\frac{50}{9}m/s$,
$\frac{50}{9}×0.2=\frac{10}{9}m$,
$\frac{10}{9}+\frac{14}{9}=\frac{8}{3}>\frac{5}{2}$
∴该车大灯的设计不能满足最小安全距离的要求.
点评 本题考查了解直角三角形,正确利用三角函数列出方程进行求解,正确理解方程思想是关键.


科目:初中数学 来源: 题型:选择题
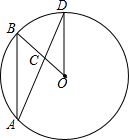 如图所示,在⊙O中,∠BOD=30°,OD∥AB,AD,OB相交于点C,那么∠BCD的度数是( )
如图所示,在⊙O中,∠BOD=30°,OD∥AB,AD,OB相交于点C,那么∠BCD的度数是( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
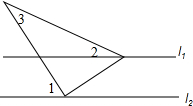 如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )
如图,直线l1∥l2,∠1=50°,∠2=23°20′,则∠3的度数为( )| A. | 26°40′ | B. | 27°20′ | C. | 27°40′ | D. | 73°20′ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com