
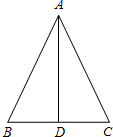
 已知,△ANC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,求:
已知,△ANC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,求:分析 (1)利用三边之间关系,可知三角形ABD是直角三角形,得出AD是高,可求△ABC的面积;
(2)再进一步利用△ABC的面积求△ABC中AB边上的高.
解答 解:(1)∵AD是中线,
∴BD=$\frac{1}{2}$BC=8,
∵BD2+AD2=64+225=289=AB2,
∴三角形ABD是直角三角形,且AD是高.
∴△ABC的面积=$\frac{1}{2}$BC×AD=$\frac{1}{2}$×16×15=120cm2.
(2)△ABC中AB边上的高=120×2÷17=$\frac{240}{17}$cm.
点评 此题考查勾股定理逆定理与三角形面积计算方法的运用,利用勾股定理逆定理判定△ABD是直角三角形是解决问题的关键.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
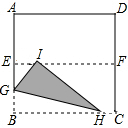 如图,将边长为4的正方形ABCD对折后展开,折痕为EF,分别在边AB、BC上取点G、H,沿GH对折,使点B落在折痕EF上,落点记为I,则:
如图,将边长为4的正方形ABCD对折后展开,折痕为EF,分别在边AB、BC上取点G、H,沿GH对折,使点B落在折痕EF上,落点记为I,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
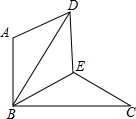 如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 北偏西68° | B. | 南偏西85° | C. | 北偏西85° | D. | 南偏西68° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com