
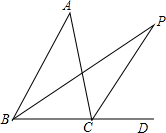
 如图,BP,CP分别平分∠ABD,∠ACD,若∠A=40°,求∠P.
如图,BP,CP分别平分∠ABD,∠ACD,若∠A=40°,求∠P. 分析 根据∠ACD=∠A+∠ABC,和CP平分∠ACD,BP平分∠ABC,得到∠PBC=$\frac{1}{2}$∠ABC,∠PCA=$\frac{1}{2}$∠ACD=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,根据∠P=180°-(∠PBC+∠PCA+∠ACB),得到$\frac{1}{2}$∠A即可.
解答 解:∵CP平分∠ACD,BP平分∠ABC,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCA=$\frac{1}{2}$∠ACD=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
∵∠P=180°-(∠PBC+∠PCA+∠ACB)=$\frac{1}{2}$∠A=20°.
点评 本题主要考查对三角形的内角和定理,三角形的外角,角平分线的定义等知识点的理解和掌握,能熟练地运用这些性质进行计算是解此题的关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:选择题
| A. | 28° | B. | 108° | C. | 118° | D. | 98° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
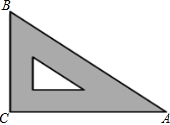 如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )
如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=$\frac{\sqrt{3}}{3}$,则边BC的长为( )| A. | 30$\sqrt{3}$cm | B. | 20$\sqrt{3}$cm | C. | 10$\sqrt{3}$cm | D. | 5$\sqrt{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
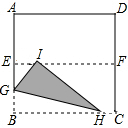 如图,将边长为4的正方形ABCD对折后展开,折痕为EF,分别在边AB、BC上取点G、H,沿GH对折,使点B落在折痕EF上,落点记为I,则:
如图,将边长为4的正方形ABCD对折后展开,折痕为EF,分别在边AB、BC上取点G、H,沿GH对折,使点B落在折痕EF上,落点记为I,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
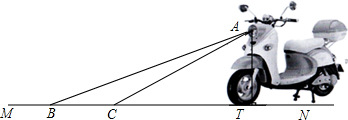
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 北偏西68° | B. | 南偏西85° | C. | 北偏西85° | D. | 南偏西68° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com