
【题目】如图,在![]() 中,
中, ![]() , 在
, 在![]() ,上取一点
,上取一点![]() ,以
,以![]() 为直径作
为直径作![]() ,与
,与![]() 相交于点
相交于点![]() ,作线段
,作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
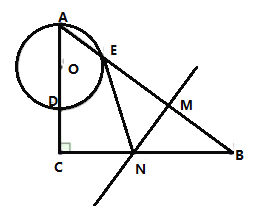
(1) 求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() 的半径为
的半径为![]() .求线段
.求线段![]() 与线段
与线段![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据题意,证出EN与OE垂直即可;
(2)求线段的长一般构造直角三角形,利用勾股定理来求解.在Rt△OEN、Rt△OCN△中,EN=ON-OE,ON=OC+CN,CN=4-EN代入可求EN;同理构造直角三角形Rt△AED、Rt△EDB、Rt△DCB,AE=AD-DE,DE=DB-BE,DB=CD+CB=1+4=17,代入求AE.
![]() 证明:连接
证明:连接![]()
![]() 是
是![]() 的垂直平分线
的垂直平分线
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 即
即![]()
![]() 是半径
是半径
![]() 是圆的切线
是圆的切线
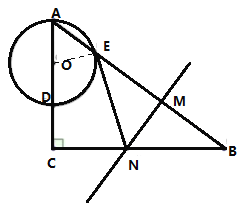
![]() 解:连接
解:连接![]()
设![]() 长为
长为![]() ,则
,则![]()
![]() ,圆的半径为
,圆的半径为![]()
![]()
![]()
![]()
解得![]() ,所以
,所以![]()
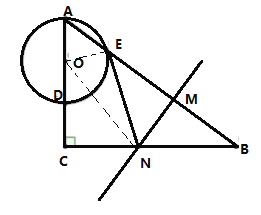
连接![]() 设
设![]()
![]()
∴AB=5,
∵AD是直径, ![]()
∴△ADE是直角三角形
则![]()
![]()
![]()
![]() 为直径,
为直径,
∴△DEB是直角三角形,
![]()
即(2-y)+(5-y) =17
解得![]()
![]()


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红将笔记本电脑水平放置在桌子上,当显示屏![]() 与底板
与底板![]() 所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图如图2. 使用时为了散热,她在底板下垫入散热架
所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图如图2. 使用时为了散热,她在底板下垫入散热架![]() 后,电脑转到
后,电脑转到![]() 位置(如图3),侧面示意图为图4. 已知
位置(如图3),侧面示意图为图4. 已知![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
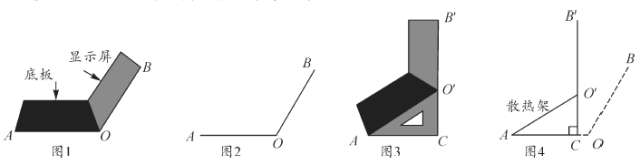
(1)求![]() 的度数.
的度数.
(2)显示屏的顶部![]() 比原来的顶部
比原来的顶部![]() 升高了多少?
升高了多少?
(3)如图4,垫入散热架后,要使显示屏![]() 与水平线的夹角仍保持120°,则显示屏
与水平线的夹角仍保持120°,则显示屏![]() 应绕点
应绕点![]() '按顺时针方向旋转多少度?并说明理由.
'按顺时针方向旋转多少度?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
(1)试判断BC与⊙O的位置关系,并说明理由;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“康河泛舟,问道剑桥”,甲乙两人相约泛舟康河,路线均为从![]() 到
到![]() 再返回
再返回![]() ,且
,且![]() 全长2千米,甲出发2分钟后,乙以另一速度出发,结果同时到达目的
全长2千米,甲出发2分钟后,乙以另一速度出发,结果同时到达目的![]() 地,甲到达目的地拍照5分钟便原速返回
地,甲到达目的地拍照5分钟便原速返回![]() 地;乙到达
地;乙到达![]() 地后休息了2分钟,然后立即提速为原速的
地后休息了2分钟,然后立即提速为原速的![]() 倍返回
倍返回![]() 地.甲乙之间的距离
地.甲乙之间的距离![]() (单位:米)与甲的行驶时间
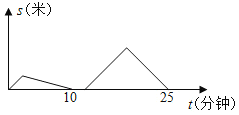
(单位:米)与甲的行驶时间![]() (单位:分钟)之间的函数关系如图所示.则当乙回到
(单位:分钟)之间的函数关系如图所示.则当乙回到![]() 地时,甲距离
地时,甲距离![]() 地________米.
地________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)求点B的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线的对称轴;
(3)已知点![]() ,
,![]() .若抛物线与线段PQ恰有一个公共点,结合函数图象,求
.若抛物线与线段PQ恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“双十一”购物街中,某儿童品牌玩具专卖店购进了![]() 两种玩具,其中
两种玩具,其中![]() 类玩具的金价比
类玩具的金价比![]() 玩具的进价每个多
玩具的进价每个多![]() 元.经调查发现:用
元.经调查发现:用![]() 元购进
元购进![]() 类玩具的数量与用
类玩具的数量与用![]() 元购进
元购进![]() 类玩具的数量相同.
类玩具的数量相同.
(1)求![]() 的进价分别是每个多少元?
的进价分别是每个多少元?
(2)该玩具店共购进![]() 了两类玩具共
了两类玩具共![]() 个,若玩具店将每个
个,若玩具店将每个![]() 类玩具定价为
类玩具定价为![]() 元出售,每个
元出售,每个![]() 类玩具定价
类玩具定价![]() 元出售,且全部售出后所获得的利润不少于
元出售,且全部售出后所获得的利润不少于![]() 元,则该淘宝专卖店至少购进
元,则该淘宝专卖店至少购进![]() 类玩具多少个?
类玩具多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com