
分析 (1)先利用零指数幂法则,绝对值及特殊角的三角函数化简,再利用实数的运算顺序求解即可,
(2)先化简,再代入求值即可.
解答 解:(1)($\sqrt{2}$-1.414)0-|$\sqrt{3}$-2|+$\root{3}{27}$-3tan30°
=1-2+$\sqrt{3}$+3-$\sqrt{3}$,
=2,
(2)($\frac{1}{x-y}$-$\frac{1}{x+y}$)÷$\frac{2y}{{x}^{2}+2xy+{y}^{2}}$,
=$\frac{x+y-(x-y)}{(x+y)(x-y)}$•$\frac{(x+y)^{2}}{2y}$,
=$\frac{x+y}{x-y}$,
当x=1+$\sqrt{2}$,y=1-$\sqrt{2}$,原式=$\frac{1+\sqrt{2}+1-\sqrt{2}}{1+\sqrt{2}-1+\sqrt{2}}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题主要考查了分式的化简求值,实数的运算,零指数幂及特殊角的三角函数,解题的关键是正确的化简及实数的运算顺序,零指数幂法则及特殊角的三角函数.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:填空题
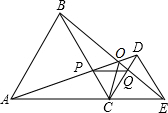 如图,C是线段AE上的一动点(不与点A、E重合)在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下六个结论:①PQ∥AE;②AP=BQ;③DE=DP;④∠AOB=60°;⑤CO平分∠AOE;⑥△CPQ为等边三角形,其中正确的是①②④⑤⑥.
如图,C是线段AE上的一动点(不与点A、E重合)在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下六个结论:①PQ∥AE;②AP=BQ;③DE=DP;④∠AOB=60°;⑤CO平分∠AOE;⑥△CPQ为等边三角形,其中正确的是①②④⑤⑥.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲班 | B. | 乙班 | ||
| C. | 两班成绩一样稳定 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)2=a2+b2 | B. | (2a-b)2=4a2-b2 | C. | (x+3)(x-2)=x2-6 | D. | (x+3)(x-3)=x2-9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 所挂物体质量x/kg | 0 | 1 | 2 | 3 | 4 | … |
| 弹簧长度y/cm | 18 | 20 | 22 | 24 | 26 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
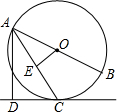 如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.
如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com