
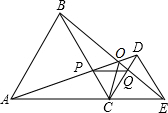
 如图,C是线段AE上的一动点(不与点A、E重合)在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下六个结论:①PQ∥AE;②AP=BQ;③DE=DP;④∠AOB=60°;⑤CO平分∠AOE;⑥△CPQ为等边三角形,其中正确的是①②④⑤⑥.
如图,C是线段AE上的一动点(不与点A、E重合)在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下六个结论:①PQ∥AE;②AP=BQ;③DE=DP;④∠AOB=60°;⑤CO平分∠AOE;⑥△CPQ为等边三角形,其中正确的是①②④⑤⑥. 分析 由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知①⑥正确;根据△CQB≌△CPA(ASA),可知②正确;根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知③错误;利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,可知④正确;⑤由BC∥DE,得到∠CBE=∠BED,由∠CBE=∠DAE,得到∠AOB=∠OAE+∠AEO=60°,同理可得出∠AOE=120°,∠OAC=∠OCD,求出∠DCE=∠AOC=60°,可知⑤正确.
解答 解:∵等边△ABC和等边△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
在△ACD与△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$
∴△ACD≌△BCE(SAS),
∴∠CBE=∠DAC,
又∵∠ACB=∠DCE=60°,
∴∠BCD=60°,即∠ACP=∠BCQ,
又∵AC=BC,
∴△CQB≌△CPA(ASA),
∴CP=CQ,
又∵∠PCQ=60°可知△PCQ为等边三角形,
故⑥正确;
∴∠PQC=∠DCE=60°,
∴PQ∥AE
故①正确,
∵△CQB≌△CPA,
∴AP=BQ,
故②正确,
∵AD=BE,AP=BQ,
∴AD-AP=BE-BQ,
即DP=QE,
∵∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,
∴∠DQE≠∠CDE,故③错误;
∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∵等边△DCE,
∠EDC=60°=∠BCD,
∴BC∥DE,
∴∠CBE=∠DEO,
∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,
故④正确.
∵BC∥DE,
∴∠CBE=∠BED,
∵∠CBE=∠DAE,
∴∠AOB=∠OAE+∠AEO=60°,
同理可得出∠AOE=120°,∠OAC=∠OCD,
∴∠DCE=∠AOC=60°,
∴OC平分∠AOE,故⑤正确;
正确的有:①②④⑤⑥.
故答案为:①②④⑤⑥.
点评 本题考查了等边三角形的性质、全等三角形的判定与性质,利用旋转不变性,找到不变量,是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
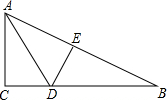 如图,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为( )
如图,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 电风扇型号 | A型 | B型 | C型 |
| 进价(元/台) | 90 | 120 | 110 |
| 售价(元/台) | 120 | 160 | 130 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com