
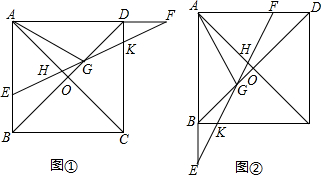
分析 (1)①过点E作EM⊥AB,交BD于点M,则EM∥AF,利用ASA证得△EMG≌△FDG后即可证得GE=GF;
②首先证明△EMG≌△FDG,得到点G为Rt△AEF斜边上的中点,则求出EF=2AG=2$\sqrt{5}$;其次,在Rt△AEF中,利用勾股定理求出BE或DF的长度;然后在Rt△DFK中解直角三角形求出DK的长度,从而得到CK的长度,由AB∥CD,列比例式求出AH的长度;最后作HN∥AE,列出比例式求出EH的长度;
(2)同理根据上题求得EK=$\frac{\sqrt{5}}{2}$,BK=$\frac{1}{2}$,AF=2,然后根据平行线分线段成比例定理求得KH=$\frac{5}{6}\sqrt{5}$,利用EH=EK+KH求得结论即可.
解答 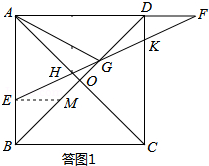 解(1)①过点E作EM⊥AB,交BD于点M,则EM∥AF,△BEM为等腰直角三角形,
解(1)①过点E作EM⊥AB,交BD于点M,则EM∥AF,△BEM为等腰直角三角形,
∵EM∥AF,
∴∠EMG=∠FDG,∠GEM=∠F;
∵△BEM为等腰直角三角形,
∴EM=BE,
∵BE=DF,
∴EM=DF.
在△EMG与△FDG中,
$\left\{\begin{array}{l}{∠EMG=∠FDG}\\{EM=DF}\\{∠GEM=∠F}\end{array}\right.$
∴△EMG≌△FDG(ASA),
∴GE=GF;
②由①GE=GF,
∴G为EF的中点,
∴EF=2AG=2$\sqrt{5}$.(直角三角形斜边上的中线长等于斜边长的一半)
设BE=DF=x,则AE=3-x,AF=3+x,
在Rt△AEF中,由勾股定理得:AE2+AF2=EF2,即(3-x)2+(3+x)2=(2$\sqrt{5}$)2,
解得x=1,即BE=1,
∴AE=2,AF=4,
∴tan∠F=$\frac{1}{2}$.
设EF与CD交于点K,则在Rt△DFK中,DK=DF•tan∠F=$\frac{1}{2}$,
,∴FK=$\sqrt{D{F}^{2}+D{K}^{2}}$=$\frac{1}{2}\sqrt{5}$,CK=CD-DK=$\frac{5}{2}$.
∴EK=EF-FK=2$\sqrt{5}$-$\frac{1}{2}\sqrt{5}$=$\frac{3}{2}\sqrt{5}$,
∵AB∥CD,
∴$\frac{EH}{HK}$=$\frac{AH}{CH}=\frac{AE}{CK}$=$\frac{2}{\frac{5}{2}}$$\frac{4}{5}$,
∴EH=$\frac{4}{9}$EK=$\frac{2}{3}\sqrt{5}$.
(2)由②得:EK=$\frac{\sqrt{5}}{2}$,BK=$\frac{1}{2}$,AF=2,
∵BK∥AD,
∴EK:EF=BK:AF,
即:$\frac{\sqrt{5}}{2}$:EF=$\frac{1}{2}$:2,
解得:EF=2$\sqrt{5}$,
∴KF=$\frac{3}{2}\sqrt{5}$,
∵BC∥AD,
∴KC:AF=KH:HF,
即:$\frac{5}{2}:2$=KH:($\frac{3}{2}\sqrt{5}$-KH),
解得:KH=$\frac{5}{6}\sqrt{5}$,
∴EH=EK+KH=$\frac{\sqrt{5}}{2}$+$\frac{5}{6}\sqrt{5}$=$\frac{4}{3}\sqrt{5}$.
点评 本题是几何综合题,考查相似三角形的综合运用,难度较大.解题关键是:第一,读懂题意,由EF与线段BD相交,可知点E、F位于直线BD的两侧,因此有两种情形,需要分类讨论,分别计算;第二,相似三角形比较多,需要理清头绪;第三,需要综合运用相似三角形、全等三角形、正方形、勾股定理、等腰直角三角形的相关性质.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:解答题
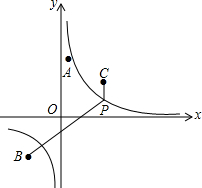 如图,点A,B,C的坐标分别为(1,5),(-4,-4),(4,4),点P为双曲线y=$\frac{8}{x}$(x>0)上一个动点.
如图,点A,B,C的坐标分别为(1,5),(-4,-4),(4,4),点P为双曲线y=$\frac{8}{x}$(x>0)上一个动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com