
【题目】已知关于x的一元二次方程x2-(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程的两个根分别为x1、x2,且满足x12+x22=31+x1x2,求实数m的值.
【答案】(1)m≥-![]() ;(2)2.
;(2)2.
【解析】
(1)根据方程有实数根结合根的判别式,即可得出关于m的一元一次不等式,解之即可得出结论;
(2)利用根与系数的关系可得出x1+x2=2m+3、x1x2=m2+2,结合x12+x22=31+x1x2即可得出关于m的一元二次方程,解之即可得出m的值.
(1)∵方程x2-(2m+3)x+m2+2=0有实数根,
∴△=[-(2m+3)]2-4(m2+2)=12m+1≥0,
解得:m≥-![]() .
.
(2)∵方程x2-(2m+3)x+m2+2=0的两个根分别为x1、x2,
∴x1+x2=2m+3,x1x2=m2+2,
∵x12+x22=31+x1x2,
∴(x1+x2)2-2x1x2=31+x1x2,即m2+12m-28=0,
解得:m1=2,m2=-14(舍去),
∴实数m的值为2.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D.
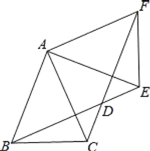
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,E为BC上一点,F为CD上一点,且AE=AF.设△AEF的面积为y,CE=x.
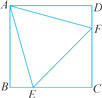
(第11题)
(1)求y关于x的函数表达式.
(2)当△AEF为正三角形时,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)过点D(0,![]() )作x轴的平行线交抛物线于E,F两点,求EF的长;
)作x轴的平行线交抛物线于E,F两点,求EF的长;
(3)当y≤![]() 时,直接写出x的取值范围是 .
时,直接写出x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】希望中学八年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩较好的甲班和乙班5名学生的比赛成绩(单位:个)
1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)求两班比赛数据的中位数;
(2)计算两班比赛数据的方差,并比较哪一个小;
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c的图象与x轴交于A(﹣5,0),B(1,0)两点,与y轴交于点C,抛物线的对称轴与x轴交于点D.
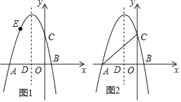
(1)求抛物线的函数表达式;
(2)如图1,点E(x,y)为抛物线上一点,且﹣5<x<﹣2,过点E作EF∥x轴,交抛物线的对称轴于点F,作EH⊥x轴于点H,得到矩形EHDF,求矩形EHDF周长的最大值;
(3)如图2,点P为抛物线对称轴上一点,是否存在点P,使以点P,A,C为顶点的三角形是直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com