练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，添加下列一个条件，不能使△ADE∽△ACB的是（ ）．

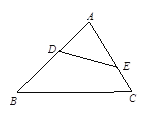
    A. DE∥BCB. ∠AED＝∠BC. ＝D. ∠ADE＝∠C

    【答案】A

    【解析】

    试题相似三角形的判定有三种方法：①三边法：三组对应边的比相等的两个三角形相似；②两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似；③两角法：有两组角对应相等的两个三角形相似。由此可得出可添加的条件：由题意得，∠A=∠A（公共角），则添加：∠ADE=∠ACB或∠AED=∠ABC，利用两角法可判定△ADE∽△ACB；故B，D正确，添加：＝，利用两边及其夹角法可判定△ADE∽△ACB，故C选项正确，当DE∥BC时，△ADE∽△ABC，AD与AB是对应边，故从对应关系来看应选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△中，，是边上的中线，于点，与交于点.

    （1）求证：；

    （2）过点作交的延长线于点.求证：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为解决楼房之间的挡光问题，某地区规定：两幢楼房间的距离至少为米，中午时不能挡光. 如图，某旧楼的一楼窗台高1米，要在此楼正南方米处再建一幢新楼. 已知该地区冬天中午时阳光从正南方照射，并且光线与水平线的夹角最小为°，在不违反规定的情况下，请问新建楼房最高_____________米. (结果精确到1米.,)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

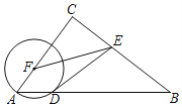
    【题目】如图，Rt△ABC中，∠C=90°，AB=4，F是线段AC上一点，过点A的⊙F交AB于点D，E是线段BC上一点，且ED=EB，则EF的最小值为_______________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

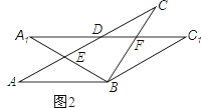
    【题目】在△ABC中，AB=BC=2，∠ABC=120°，将△ABC绕点B顺时针旋转角α（0°＜α＜90°）得△A1BC1，A1B交AC于点E，A1C1分别交AC、BC于D、F两点．

    （1）如图1，观察并猜想，在旋转过程中，线段BE与BF有怎样的数量关系？并证明你的结论；

    （2）如图2，当α=30°时，试判断四边形BC1DA的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以半圆中的一条弦BC（非直径）为对称轴将弧BC折叠后与直径AB交于点D，若＝，且AB＝10，则CB的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，二次函数的图象与x轴交于A、B两点，其中A点坐标为，点，另抛物线经过点，M为它的顶点．

    求抛物线的解析式；

    求的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2-（2m+3）x+m2+2=0．
    （1）若方程有实数根，求实数m的取值范围；
    （2）若方程的两个根分别为x1、x2，且满足x12+x22=31+x1x2，求实数m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．

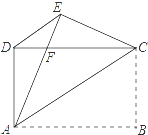
    （1）求证：△ADE≌△CED；

    （2）求证：△DEF是等腰三角形．

    查看答案和解析>>

    同步练习册答案