
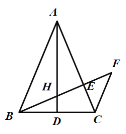
【题目】已知:如图,在△![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上的中线,
上的中线,![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]()
【答案】(1)见解析;(2)见解析
【解析】
(1)由三线合一可证BD=CD,然后通过证明△BDH∽△ADC,即可证明结论成立;
(2)连接CH,由等腰三角形的性质可证∠ABH=∠ACH.根据平行线的性质定理得到∠BFC=∠FBA,从而∠BFC=∠ECH;然后可证△CFH∽△ECH,并根据相似三角形的性质定理与等量代换得到结论.
(1)∵![]() ,
,![]() 是边
是边![]() 上的中线,
上的中线,
∴AD⊥BC,BD=CD,
∴∠ACD+∠CAD=90°.
∵![]() ,
,
∴∠EBD+∠ACB=90°,
∴∠CAD=∠CBD,
∵∠BDH=∠CDH=90°,
∴△BDH∽△ADC,
∴![]() ,
,
∴![]() ;
;
(2)如图所示,连接CH.
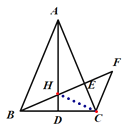
∵AD⊥BC,BD=CD,
∴AD垂直平分BC,
∴BH=CH,
∴∠HBD=∠HCD,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABH=∠ACH.
∵AB∥CF,
∴∠BFC=∠FBA.
∴∠BFC=∠ECH.
在△CFH与△ECH中,
∵∠BFC=∠ECH,∠CHE=∠CHF,
∴△CFH∽△ECH,
∴CH:HE=HF:CH.
又∵BH=CH,
∴BH2=HE·HF.


科目:初中数学 来源: 题型:
【题目】某数学课外兴趣小组成员在研究下面三个有联系的问题,请你帮助他们解决:
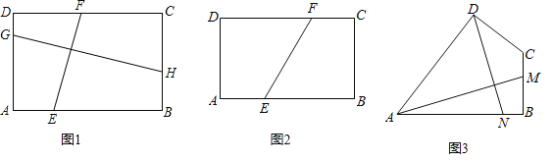
(1)如图1,矩形ABCD中,AB=a,BC=b,点E,F分别在AB,DC上,点G,H分别在AD,BC上且EF⊥GH,求![]() 的值.
的值.
(2)如图2,矩形ABCD中,AB=4,BC=3,将矩形对折,使得B、D重叠,折痕为EF,求EF的长.
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=8,BC=CD=4,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
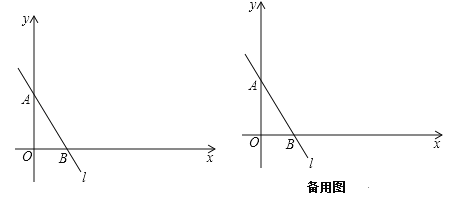
【题目】如图,已知一次函数y=﹣![]() x+4的图象是直线l,设直线l分别与y轴、x轴交于点A、B.
x+4的图象是直线l,设直线l分别与y轴、x轴交于点A、B.
(1)求线段AB的长度;
(2)设点M在射线AB上,将点M绕点A按逆时针方向旋转90°到点N,以点N为圆心,NA的长为半径作⊙N.
①当⊙N与x轴相切时,求点M的坐标;
②在①的条件下,设直线AN与x轴交于点C,与⊙N的另一个交点为D,连接MD交x轴于点E,直线m过点N分别与y轴、直线l交于点P、Q,当△APQ与△CDE相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D.
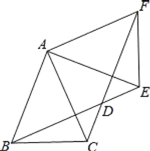
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com