
ЁОЬтФПЁПФГЪ§бЇПЮЭтаЫШЄаЁзщГЩдБдкбаОПЯТУцШ§ИігаСЊЯЕЕФЮЪЬтЃЌЧыФуАяжњЫћУЧНтОіЃК
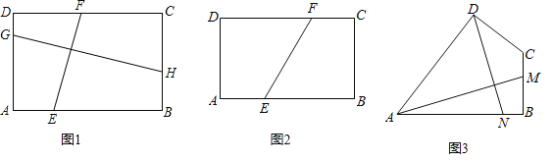
ЃЈ1ЃЉШчЭМ1ЃЌОиаЮABCDжаЃЌABЃНaЃЌBCЃНbЃЌЕуEЃЌFЗжБ№дкABЃЌDCЩЯЃЌЕуGЃЌHЗжБ№дкADЃЌBCЩЯЧвEFЁЭGHЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
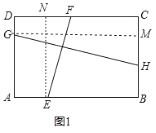
ЃЈ2ЃЉШчЭМ2ЃЌОиаЮABCDжаЃЌABЃН4ЃЌBCЃН3ЃЌНЋОиаЮЖделЃЌЪЙЕУBЁЂDжиЕўЃЌелКлЮЊEFЃЌЧѓEFЕФГЄЃЎ
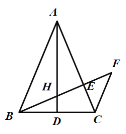
ЃЈ3ЃЉШчЭМ3ЃЌЫФБпаЮABCDжаЃЌЁЯABCЃН90ЁуЃЌABЃНADЃН8ЃЌBCЃНCDЃН4ЃЌAMЁЭDNЃЌЕуMЃЌNЗжБ№дкБпBCЃЌABЩЯЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуGзїGMЁЭCBгкMЃЌЙ§ЕуEзїENЁЭCDгкЕуNЃЌПЩжЄЫФБпаЮDCMGЪЧОиаЮЃЌЫФБпаЮABMGЪЧОиаЮЃЌЫФБпаЮAENDЪЧОиаЮЃЌЫФБпаЮBCNEЪЧОиаЮЃЌПЩЕУGM=CD=ABЃЌEN=AD=BCЃЌЭЈЙ§жЄУїЁїEFNЁзЁїGHMЃЌПЩЧѓНтЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгBDНЛEFгкЕуOЃЌDEЃЌBFЃЌПЩжЄЫФБпаЮDFBEЪЧСтаЮЃЌПЩЕУBO=DOЃЌEO=FOЃЌBDЁЭEFЃЌгЩЙДЙЩЖЈРэПЩЧѓDEЃЌDOЃЌEOЕФГЄЃЌМДПЩЧѓEFЕФГЄЃЛ
ЃЈ3ЃЉЙ§ЕуDзїEFЁЭBCЃЌНЛBCЕФбгГЄЯпгкFЃЌЙ§ЕуAзїAEЁЭEFЃЌСЌНгACЃЌгЩЁАSSSЁБПЩжЄЁїACDЁеЁїACBЃЌПЩЕУЁЯADC=ЁЯABC=90ЁуЃЌЭЈЙ§жЄУїЁїADEЁзЁїDCFЃЌПЩЕУAE=2DFЃЌDE=2CFЃЌгЩЙДЙЩЖЈРэПЩЧѓDEЕФГЄЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуGзїGMЁЭCBгкMЃЌЙ§ЕуEзїENЁЭCDгкЕуNЃЌ
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯAЃНЁЯBЃНЁЯCЃНЁЯDЃН90ЁуЃЌABЃНCDЃЌADЃНBCЃЌЧвGMЁЭBCЃЌENЁЭCDЃЌ
ЁрЫФБпаЮDCMGЪЧОиаЮЃЌЫФБпаЮABMGЪЧОиаЮЃЌЫФБпаЮAENDЪЧОиаЮЃЌЫФБпаЮBCNEЪЧОиаЮЃЌ
ЁрGMЃНCDЃНABЃЌENЃНADЃНBCЃЌ
ЁпEFЁЭGHЃЌЁЯBCDЃН90ЁуЃЌ
ЁрЁЯEFC+ЁЯGHCЃН180ЁуЃЌЧвЁЯDFE+ЁЯEFCЃН180ЁуЃЌ
ЁрЁЯEFNЃНЁЯGHCЃЌЧвЁЯENFЃНЁЯGMHЃН90ЁуЃЌ
ЁрЁїEFNЁзЁїGHMЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгBDНЛEFгкЕуOЃЌDEЃЌBFЃЌ
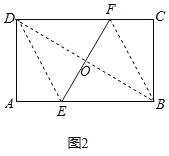
ЁпНЋОиаЮЖделЃЌЪЙЕУBЁЂDжиЕўЃЌ
ЁрBEЃНDEЃЌЁЯDEFЃНЁЯBEFЃЌ
ЁпABЁЮCDЃЌ
ЁрЁЯDFEЃНЁЯBEFЃЌ
ЁрЁЯDFEЃНЁЯDEFЃЌ
ЁрDFЃНDEЃЌЧвBEЃНDEЃЌ
ЁрBEЃНDFЃЌЧвABЁЮCDЃЌ
ЁрЫФБпаЮDFBEЪЧЦНааЫФБпаЮЃЌЧвDFЃНDEЃЌ
ЁрЫФБпаЮDFBEЪЧСтаЮЃЌ
ЁрBOЃНDOЃЌEOЃНFOЃЌBDЁЭEFЃЌ
ЁпDE2ЃНAE2+AD2ЃЌ
ЁрDE2ЃН9+ЃЈ4ЉDEЃЉ2ЃЌ
ЁрDEЃН![]() ЃЌ
ЃЌ
ЁпBDЃН![]() ЃН
ЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁрDOЃНBOЃН![]() ЃЌ
ЃЌ
ЁрOEЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрEFЃН2OEЃН![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЙ§ЕуDзїEFЁЭBCЃЌНЛBCЕФбгГЄЯпгкFЃЌЙ§ЕуAзїAEЁЭEFЃЌСЌНгACЃЌ
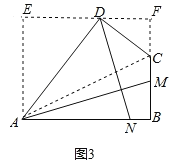
ЁпЁЯABCЃН90ЁуЃЌAEЁЭEFЃЌEFЁЭBCЃЌ
ЁрЫФБпаЮABFEЪЧОиаЮЃЌ
ЁрЁЯEЃНЁЯFЃН90ЁуЃЌAEЃНBFЃЌEFЃНABЃН8ЃЌ
ЁпADЃНABЃЌBCЃНCDЃЌACЃНACЃЌ
ЁрЁїACDЁеЁїACBЃЈSSSЃЉ
ЁрЁЯADCЃНЁЯABCЃН90ЁуЃЌ
ЁрЁЯADE+ЁЯCDFЃН90ЁуЃЌЧвЁЯADE+ЁЯEADЃН90ЁуЃЌ
ЁрЁЯEADЃНЁЯCDFЃЌЧвЁЯEЃНЁЯFЃН90ЁуЃЌ
ЁрЁїADEЁзЁїDCFЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAEЃН2DFЃЌDEЃН2CFЃЌ
ЁпDC2ЃНCF2+DF2ЃЌ
Ёр16ЃНCF2+ЃЈ8Љ2CFЃЉ2ЃЌ
ЁрDEЃН4ЃЈВЛКЯЬтвтЩсШЅЃЉЃЌDEЃН![]() ЃЌ
ЃЌ
ЁрBFЃНBC+CFЃН![]() ЃНAEЃЌ
ЃНAEЃЌ
гЩЃЈ1ЃЉПЩжЊЃК![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ


 ХргХШ§КУЩњЯЕСаД№АИ
ХргХШ§КУЩњЯЕСаД№АИ гХЛЏзївЕЩЯКЃПЦММЮФЯзГіАцЩчЯЕСаД№АИ
гХЛЏзївЕЩЯКЃПЦММЮФЯзГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
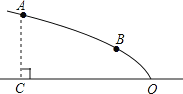
ЁОЬтФПЁПШчЭМЃЌФГЙуГЁЩшМЦЕФвЛНЈжўЮядьаЭЕФзнНиУцЪЧХзЮяЯпЕФвЛВПЗжЃЌХзЮяЯпЕФЖЅЕуOТфдкЫЎЦНУцЩЯЃЌЖдГЦжсЪЧЫЎЦНЯпOCЃЎЕуAЁЂBдкХзЮяЯпдьаЭЩЯЃЌЧвЕуAЕНЫЎЦНУцЕФОрРыAC=4УзЃЌЕуBЕНЫЎЦНУцОрРыЮЊ2УзЃЌOC=8УзЃЎ
ЃЈ1ЃЉЧыНЈСЂЪЪЕБЕФжБНЧзјБъЯЕЃЌЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЮЊСЫАВШЋУРЙлЃЌЯжашдкЫЎЦНЯпOCЩЯеввЛЕуPЃЌгУжЪЕиЁЂЙцИёвбШЗЖЈЕФдВаЮИжЙмжЦзїСНИљжЇжљPAЁЂPBЖдХзЮяЯпдьаЭНјаажЇГХМгЙЬЃЌФЧУДдѕбљВХФмевЕНСНИљжЇжљгУСЯзюЪЁЃЈжЇжљгыЕиУцЁЂдьаЭЖдНгЗНЪНЕФгУСЯЖрЩйЮЪЬтднВЛПМТЧЃЉЪБЕФЕуPЃПЃЈЮоашжЄУїЃЉ
ЃЈ3ЃЉЮЊСЫЪЉЙЄЗНБуЃЌЯжашМЦЫуГіЕуOЁЂPжЎМфЕФОрРыЃЌФЧУДСНИљжЇжљгУСЯзюЪЁЪБЕуOЁЂPжЎМфЕФОрРыЪЧЖрЩйЃПЃЈВЛаДЧѓНтЙ§ГЬЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
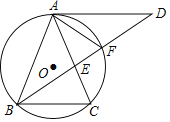
ЁОЬтФПЁПШчЭМЃЌЁїABCФкНггкЁбOЃЌAB=ACЃЌЁЯBAC=36ЁуЃЌЙ§ЕуAзїADЁЮBCЃЌгыЁЯABCЕФЦНЗжЯпНЛгкЕуDЃЌBDгыACНЛгкЕуEЃЌгыЁбOНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓЁЯDAFЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓжЄЃКAE2=EFEDЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊyЃНЉxЃЈx+3ЉaЃЉ+1ЪЧЙигкxЕФЖўДЮКЏЪ§ЃЌЕБ1ЁмxЁм5ЪБЃЌШчЙћyдкxЃН1ЪБШЁЕУзюаЁжЕЃЌдђЪЕЪ§aЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЁїABCдкжБНЧзјБъЦНУцФкЃЌШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈ0ЃЌ3ЃЉЁЂBЃЈ3ЃЌ4ЃЉЁЂCЃЈ2ЃЌ2ЃЉЃЈе§ЗНаЮЭјИёжаУПИіаЁе§ЗНаЮЕФБпГЄЪЧвЛИіЕЅЮЛГЄЖШЃЉЃЎ
ЃЈ1ЃЉЛГіЁїABCЯђЯТЦНвЦ4ИіЕЅЮЛГЄЖШЕУЕНЕФЁїA1B1C1ЃЌЕуC1ЕФзјБъЪЧЁЁ ЃЛ
ЃЈ2ЃЉвдЕуBЮЊЮЛЫЦжааФЃЌдкЭјИёФкЛГіЁїA2B2C2ЃЌЪЙЁїA2B2C2гыЁїABCЮЛЫЦЃЌЧвЮЛЫЦБШЮЊ2ЃК1ЃЌЕуC2ЕФзјБъЪЧЁЁ ЁЁЃЛ
ЃЈ3ЃЉЁїA2B2C2ЕФУцЛ§ЪЧЁЁ ЁЁЦНЗНЕЅЮЛЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЬЖгдкЮвЪаЪЕЪЉХяЛЇЧјИФдьЙ§ГЬжаГаАќСЫвЛЯюВ№ЧЈЙЄГЬЃЎдМЦЛЎУПЬьВ№ЧЈ![]() ЃЌвђЮЊзМБИЙЄзїВЛзуЃЌЕквЛЬьЩйВ№ЧЈСЫ
ЃЌвђЮЊзМБИЙЄзїВЛзуЃЌЕквЛЬьЩйВ№ЧЈСЫ![]() ЃЎДгЕкЖўЬьПЊЪМЃЌИУЙЄГЬЖгМгПьСЫВ№ЧЈЫйЖШЃЌЕкШ§ЬьВ№ЧЈСЫ
ЃЎДгЕкЖўЬьПЊЪМЃЌИУЙЄГЬЖгМгПьСЫВ№ЧЈЫйЖШЃЌЕкШ§ЬьВ№ЧЈСЫ![]() ЃЎЧѓЃК
ЃЎЧѓЃК
![]() ИУЙЄГЬЖгЕквЛЬьВ№ЧЈЕФУцЛ§ЃЛ
ИУЙЄГЬЖгЕквЛЬьВ№ЧЈЕФУцЛ§ЃЛ
![]() ШєИУЙЄГЬЖгЕкЖўЬьЁЂЕкШ§ЬьУПЬьЕФВ№ЧЈУцЛ§БШЧАвЛЬьдіМгЕФАйЗжЪ§ЯрЭЌЃЌЧѓетИіАйЗжЪ§ЃЎ
ШєИУЙЄГЬЖгЕкЖўЬьЁЂЕкШ§ЬьУПЬьЕФВ№ЧЈУцЛ§БШЧАвЛЬьдіМгЕФАйЗжЪ§ЯрЭЌЃЌЧѓетИіАйЗжЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌКЏЪ§y=![]() ЕФЭМЯёгыxЁЂyжсЗжБ№НЛгкЕуAЁЂB.вдABЮЊжБОЖзї
ЕФЭМЯёгыxЁЂyжсЗжБ№НЛгкЕуAЁЂB.вдABЮЊжБОЖзї![]() M.
M.
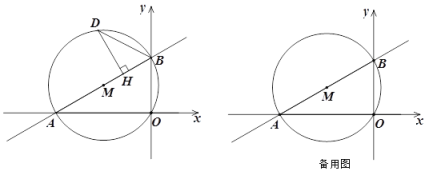
ЃЈ1ЃЉЧѓABЕФГЄЃЛ
ЃЈ2ЃЉЕуDЪЧ![]() MЩЯШЮвтвЛЕуЃЌЧвЕуDдкжБЯпABЩЯЗНЃЌЙ§ЕуDзїDHЁЭABЃЌДЙзуЮЊHЃЌСЌНгBD.
MЩЯШЮвтвЛЕуЃЌЧвЕуDдкжБЯпABЩЯЗНЃЌЙ§ЕуDзїDHЁЭABЃЌДЙзуЮЊHЃЌСЌНгBD.
ЂйЕБЁїBDHжагавЛИіНЧЕШгк![]() BAOСНБЖЪБЃЌЧѓЕуDЕФзјБъЃЛ
BAOСНБЖЪБЃЌЧѓЕуDЕФзјБъЃЛ
ЂкЕБ![]() DBH=45ЁуЪБЃЌЧѓЕуDЕФзјБъ.
DBH=45ЁуЪБЃЌЧѓЕуDЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
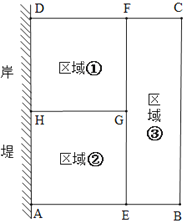
ЁОЬтФПЁПЮЊСЫНкЪЁВФСЯЃЌФГЫЎВњбјжГЛЇРћгУЫЎПтЕФАЖЕЬ(АЖЕЬзуЙЛГЄ)ЮЊвЛБпЃЌгУзмГЄЮЊ80УзЕФЮЇЭјдкЫЎПтжаЮЇГЩСЫШчЭМЫљЪОЕФЂйЂкЂлШ§ПщОиаЮЧјгђЃЌЖјЧвAEЃКBE=2:1.ЩшBCЕФГЄЖШЪЧ![]() УзЃЌОиаЮЧјгђABCDЕФУцЛ§ЮЊ
УзЃЌОиаЮЧјгђABCDЕФУцЛ§ЮЊ![]() ЦНЗНУз.
ЦНЗНУз.
(1)Чѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂзЂУїздБфСП
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂзЂУїздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
(2)![]() ШЁКЮжЕЪБЃЌ
ШЁКЮжЕЪБЃЌ![]() газюДѓжЕЃПзюДѓжЕЪЧЖрЩйЃП
газюДѓжЕЃПзюДѓжЕЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкЁї![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧБп
ЪЧБп![]() ЩЯЕФжаЯпЃЌ
ЩЯЕФжаЯпЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() .
.
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() .ЧѓжЄЃК
.ЧѓжЄЃК![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com