
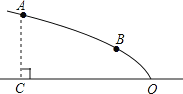
����Ŀ����ͼ��ij�㳡��Ƶ�һ���������͵��ݽ����������ߵ�һ���֣������ߵĶ���O����ˮƽ���ϣ��Գ�����ˮƽ��OC����A��B�������������ϣ��ҵ�A��ˮƽ��ľ���AC=4�ף���B��ˮƽ�����Ϊ2�ף�OC=8�ף�
��1���뽨���ʵ���ֱ������ϵ���������ߵĺ�������ʽ��
��2��Ϊ�˰�ȫ���ۣ�������ˮƽ��OC����һ��P�����ʵء������ȷ����Բ�θֹ���������֧��PA��PB�����������ͽ���֧�żӹ̣���ô���������ҵ�����֧��������ʡ��֧������桢���ͶԽӷ�ʽ�����϶��������ݲ����ǣ�ʱ�ĵ�P��������֤����
��3��Ϊ��ʩ�����㣬����������O��P֮��ľ��룬��ô����֧��������ʡʱ��O��P֮��ľ����Ƕ��٣�����д�����̣�
���𰸡���1�������ߵĺ�������ʽΪ��y=![]() x2��
x2��
��2���ҷ�������
��3������֧��������ʡʱ����O��P֮��ľ�����4�ף�
��������
��1������������Խ������ʵ�ƽ��ֱ������ϵ���Ӷ�������������ߵĽ���ʽ��
��2����������֮���߶���࣬������Ӧ��ͼ�Σ�д���������ɣ�
��3������ǰ�������ϵ�������߽���ʽ������õ�B�����꣬�ٸ������������ƿ����������֧��������ʡʱ��O��P֮��ľ��룬ע��˴�ֻд���𰸼��ɣ�
�⣺��1����ͼ��
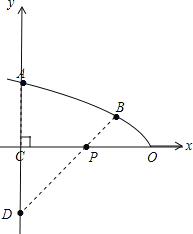
�Ե�OΪԭ�㡢����OCΪy��������Ὠ��ֱ������ϵ��
�������ߵĺ�������ʽΪy=ax2��
������֪��A������Ϊ��4��8����
�ߵ�A���������ϣ�
��8=a��42��
���a=![]() ��
��
�����������ߵĺ�������ʽΪ��y=![]() x2��
x2��
��2���ҷ���
�ӳ�AC�������������������������ڵ�D��
���A��D����OC�Գƣ�
����BD��OC�ڵ�P�����P��Ϊ����
��3������ͼ��������֪��B�ĺ�����Ϊ2��
�ߵ�B���������ϣ�
���B��������2��2����
�֡ߵ�A������Ϊ��4��8����
���D����������4��8����
��ֱ��BD�ĺ�������ʽΪy=kx+b��
��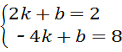 ��
��
��ã�k=��1��b=4��
��ֱ��BD�ĺ�������ʽΪy=��x+4��
��x=0����y=��x+4���õ�P������Ϊ��0��4����
����֧��������ʡʱ����O��P֮��ľ�����4�ף�



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ȱ���ABC�Ƶ�C˳ʱ����ת120���õ���EDC������AD��BD�������н��ۣ�
��AC=AD����BD��AC�����ı���ACED�����Σ�
������ȷ�ĸ����ǣ� ��

A��0 B��1 C��2 D��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�D��BC�ϣ���AD=BD��AB=AC=CD�����BAC=_________
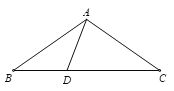
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У�ACΪ�Խ��ߣ���DAC����BCA����AD��BC��CD��AD�ڵ�D��
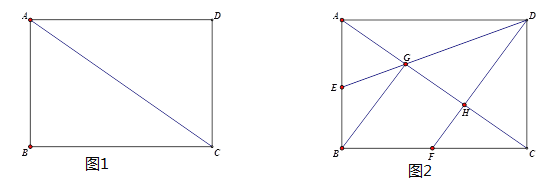
��1����ͼ1����֤���ı���ABCD�Ǿ��Ρ�
��2����ͼ2����E�͵�F�ֱ�Ϊ��AB�ͱ�BC���е㣬����DE��DF�ֱ�AC�ڵ�G�͵�H������BG���ڲ����������߶ε�����£���д�������������FHC�����2�������������Ρ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y����x2+x+2��x���ڵ�A.B��A��B���Ҳࣩ����y�ύ�ڵ�C��DΪ��һ�����������ϵĶ��㣬���ACD��������ֵ��_____
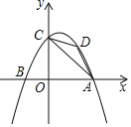
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
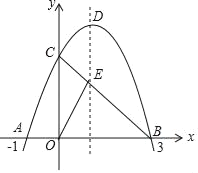
����Ŀ����ͼ����֪������y=��x2+bx+c��x�ύ�ڵ�A����1��0���͵�B��3��0������y�ύ�ڵ�C������BC�������ߵĶԳ����ڵ�E��D�������ߵĶ��㣮
��1����������ߵĽ���ʽ��
��2�����C�͵�D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
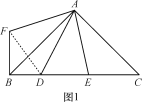
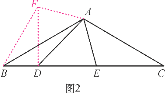
����Ŀ��(1)��ͼ1����ABC�У���BAC��90�㣬AB��AC��D��E��BC�ϣ���DAE��45�㣬Ϊ��̽��BD��DE��CE֮��ĵ�����ϵ���ֽ���AEC��A˳ʱ����ת90���ɡ�AFB������DF����̽���������õ���BD��DE��CE֮��ĵ�����ϵʽ�� ��(����֤��)
(2)��ͼ2���ڡ�ABC�У���BAC��120�㣬AB��AC��D��E��BC�ϣ���DAE��60�㣬��ADE��45�㣬�Է���(1)�ķ���������ͼ�ε���ת�任��̽��BD��DE��CE֮��ĵ�����ϵ����֤����Ľ��ۣ�
 ������������
������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ϫũ���Ŵ�Ϊ���¸���С����������չ��ͥ��ֳҵ.������![]() ����ľ��Χһ�����ε���Ȧ��Ϊ�˽�Լ����ͬʱҪʹ���ε����������������Լҷ���һ�泤
����ľ��Χһ�����ε���Ȧ��Ϊ�˽�Լ����ͬʱҪʹ���ε����������������Լҷ���һ�泤![]() ��ǽ���������ͼ��ʾ��һ��������Ȧ.
��ǽ���������ͼ��ʾ��һ��������Ȧ.
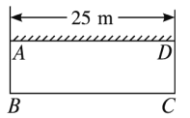
��1����������Ŵľ�����Ȧ�������
��2�������ж�������Ʒ����Ƿ���������������ֱ�Ӵ����������������ָ������ƣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������ȤС���Ա���о�������������ϵ�����⣬����������ǽ����
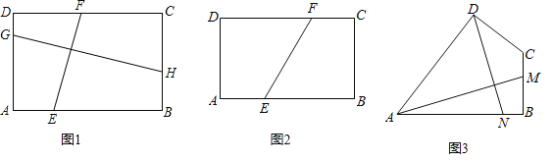
��1����ͼ1������ABCD�У�AB��a��BC��b����E��F�ֱ���AB��DC�ϣ���G��H�ֱ���AD��BC����EF��GH����![]() ��ֵ��
��ֵ��
��2����ͼ2������ABCD�У�AB��4��BC��3�������ζ��ۣ�ʹ��B��D�ص����ۺ�ΪEF����EF�ij���
��3����ͼ3���ı���ABCD�У���ABC��90����AB��AD��8��BC��CD��4��AM��DN����M��N�ֱ��ڱ�BC��AB�ϣ���![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com