
【题目】安徽郎溪农民张大伯为了致富奔小康,大力发展家庭养殖业.他准备用![]() 长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长
长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长![]() 的墙,设计了如图所示的一个矩形羊圈.
的墙,设计了如图所示的一个矩形羊圈.
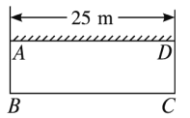
(1)请你求出张大伯的矩形羊圈的面积;
(2)请你判断他的设计方案是否合理?如果合理,直接答合理;如果不合理又该如何设计?并说明理由.
科目:初中数学 来源: 题型:
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=![]() (BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
(BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
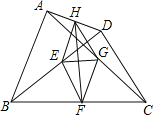
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
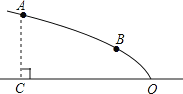
【题目】如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O落在水平面上,对称轴是水平线OC.点A、B在抛物线造型上,且点A到水平面的距离AC=4米,点B到水平面距离为2米,OC=8米.
(1)请建立适当的直角坐标系,求抛物线的函数解析式;
(2)为了安全美观,现需在水平线OC上找一点P,用质地、规格已确定的圆形钢管制作两根支柱PA、PB对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点P?(无需证明)
(3)为了施工方便,现需计算出点O、P之间的距离,那么两根支柱用料最省时点O、P之间的距离是多少?(不写求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)当![]() 时,利用根的判别式判断方程根的情况;
时,利用根的判别式判断方程根的情况;
(2)若方程有两个相等的实数根,请写出一组满足条件的![]() 的值,并求出此时方程的根.
的值,并求出此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动(抛物线随顶点一起平移),与
上运动(抛物线随顶点一起平移),与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),点
的左侧),点![]() 的横坐标最小值为-6,则点
的横坐标最小值为-6,则点![]() 的横坐标最大值为( )
的横坐标最大值为( )
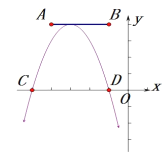
A.-3B.1C.5D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,已知折痕与边BC交于点O,连结AP、OP、OA.

(1)求证:△OCP∽△PDA;
(2)若△OCP与△PDA的面积比为1:4,求边AB的长;
(3)如图2,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.探究:当点M、N在移动过程中,线段EF与线段PB有何数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
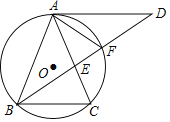
【题目】如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)求∠DAF的度数;
(2)求证:AE2=EFED;
查看答案和解析>>
科目:初中数学 来源: 题型:
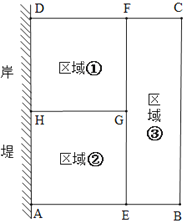
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且AE:BE=2:1.设BC的长度是![]() 米,矩形区域ABCD的面积为
米,矩形区域ABCD的面积为![]() 平方米.
平方米.
(1)求![]() 与
与![]() 之间的函数关系式,并注明自变量
之间的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)![]() 取何值时,
取何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com