
【题目】如图,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动(抛物线随顶点一起平移),与
上运动(抛物线随顶点一起平移),与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),点
的左侧),点![]() 的横坐标最小值为-6,则点
的横坐标最小值为-6,则点![]() 的横坐标最大值为( )
的横坐标最大值为( )
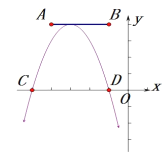
A.-3B.1C.5D.8
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
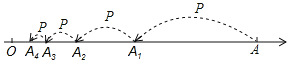
【题目】数轴上OA两点的距离为4,一动点P从A点出发按以下规律跳动:第一次跳动到AO的中点A1处,第二次从A1点跳动到A1O的中点A2处,第三次从A2跳动到A2O的中点A3处按照这样的规律,继续跳动到点A4A5A6……An(n≥3,n是整数)处那么线段A3O的长度为_________,AnA的长度为_________ 。
查看答案和解析>>
科目:初中数学 来源: 题型:
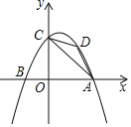
【题目】如图,二次函数y=﹣x2+x+2交x轴于点A.B(A在B的右侧),与y轴交于点C,D为第一象限抛物线上的动点,则△ACD面积的最大值是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
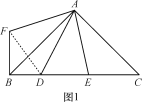
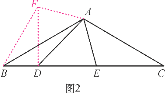
【题目】(1)如图1,△ABC中,∠BAC=90°,AB=AC,D,E在BC上,∠DAE=45°,为了探究BD,DE,CE之间的等量关系,现将△AEC绕A顺时针旋转90°后成△AFB,连接DF,经探究,你所得到的BD,DE,CE之间的等量关系式是 ;(无须证明)
(2)如图2,在△ABC中,∠BAC=120°,AB=AC,D,E在BC上,∠DAE=60°,∠ADE=45°,试仿照(1)的方法,利用图形的旋转变换,探究BD,DE,CE之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在该抛物线上(
在该抛物线上(![]() 点与
点与![]() ,
,![]() 两点不重合),如果
两点不重合),如果![]() 的三边满足
的三边满足![]() ,则称点
,则称点![]() 为抛物线
为抛物线![]() (
(![]() )的勾股点.
)的勾股点.
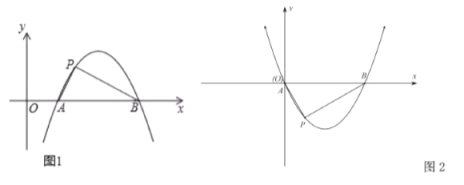
(1)求证:点![]() 是抛物线
是抛物线![]() 的勾股点.
的勾股点.
(2)如图2,已知抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 的勾股点,求抛物线
的勾股点,求抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】安徽郎溪农民张大伯为了致富奔小康,大力发展家庭养殖业.他准备用![]() 长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长
长的木栏围一个矩形的羊圈,为了节约材料同时要使矩形的面积最大,他利用了自家房屋一面长![]() 的墙,设计了如图所示的一个矩形羊圈.
的墙,设计了如图所示的一个矩形羊圈.
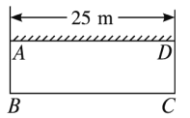
(1)请你求出张大伯的矩形羊圈的面积;
(2)请你判断他的设计方案是否合理?如果合理,直接答合理;如果不合理又该如何设计?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>![]() 时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
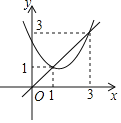
A. ①②④B. ②③④C. ②④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为实数)
为实数)
(1)当![]() 时,若
时,若![]() = ,则此函数是一次函数;
= ,则此函数是一次函数;
(2)若它是一个二次函数,假设![]() ,那么:
,那么:
①当![]() 时,
时,![]() 随
随![]() 的增大而减小,请判断这个命题的真假并说明理由;
的增大而减小,请判断这个命题的真假并说明理由;
②它一定经过哪个点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com