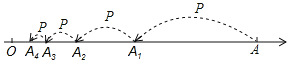
【题目】数轴上OA两点的距离为4，一动点P从A点出发按以下规律跳动：第一次跳动到AO的中点A1处，第二次从A1点跳动到A1O的中点A2处，第三次从A2跳动到A2O的中点A3处按照这样的规律，继续跳动到点A4A5A6……An（n≥3，n是整数）处那么线段A3O的长度为_________，AnA的长度为_________ 。
教材全解字词句篇系列答案科目：初中数学 来源： 题型：
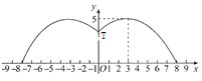
【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系
(1)求水柱所在抛物线(第一象限部分)的函数解析式
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿？
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某市郊外景区内一条笔直的公路a经过三个景点A、B、C，景区管委会又开发了风景优美的景点D，经测量景点D位于景点A的北偏东30°方向8km处，位于景点B的正北方向，还位于景点C的北偏西75°方向上，已知AB=5km．
（1）景区管委会准备由景点D向公路a修建一条距离最短的公路，不考虑其它因素，求出这条公路的长；（结果精确到0.1km）
（2）求景点C与景点D之间的距离．（结果精确到1km）
（参考数据：
=1.73，
=2.24，sin53°=cos37°=0.80，sin37°=cos53°=0.60，tan53°=1.33，tan37°=0.75，sin38°=cos52°=0.62，sin52°=cos38°=0.79，tan38°=0.78，tan52°=1.28，sin75°=0.97，cos75°=0.26，tan75°=3.73．）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
图象的顶点坐标为（3，8），该二次函数图象的对称轴与x轴的交点为A，M是这个二次函数图象上的点，O是原点．
（1）不等式b+2c+8≥0是否成立？请说明理由；
（2）设S是△AMO的面积，求满足S=9的所有点M的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB＞AC，点D、E分别是边AB、AC的中点，点F在BC边上，连接DE、DF、EF，则添加下列哪一个条件后，仍无法判断△FCE与△EDF全等（ ）
A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，E、F、G、H分别是BD、BC、AC、AD的中点，且AB＝CD．下列结论：①EG⊥FH，②四边形EFGH是矩形，③HF平分∠EHG，④EG＝
(BC－AD)，⑤四边形EFGH是菱形．其中正确的个数是 ( )
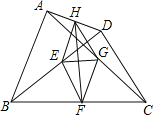
A．1 B．2 C．3 D．4
查看答案和解析>>
科目：初中数学 来源： 题型：
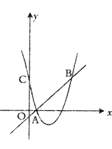
【题目】如图，抛物线
与直线
交于点
，点
，与
轴交于点
.
（1）求
的值和抛物线的解析式；
（2）直接写出方程
的解；
（3）点
是抛物线对称轴上的一个动点，当
的值最小时，判断
的形状.
查看答案和解析>>
科目：初中数学 来源： 题型：
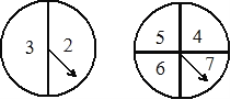
【题目】红和小华都想去参加学校组织的演讲比赛，但现在名额只有一个，于是小英想出了一个办法：让小红和小华分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被四等分)，在两个转盘都停止转动后，若指针所指的两个数字之和为偶数，则小红去；若指针所指的两个数字之和为奇数，则小华去，你认为这个方法公平吗?请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
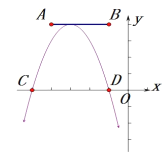
【题目】如图，点
，
的坐标分别为
和
，抛物线
的顶点在线段
上运动（抛物线随顶点一起平移），与
轴交于
、
两点（在的左侧），点的横坐标最小值为-6，则点的横坐标最大值为（ ）
A.-3B.1C.5D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
