
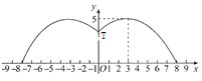
【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系
(1)求水柱所在抛物线(第一象限部分)的函数解析式
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿?
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度
【答案】(1)![]() ;(2)为了不被淋湿,身高1.8米的人站立时必须在离水池中心7米以内;(3)
;(2)为了不被淋湿,身高1.8米的人站立时必须在离水池中心7米以内;(3)![]()
【解析】
(1)根据顶点坐标可设二次函数的顶点式,代入(8,0)即可求得a,此题得解;
(2)利用二次函数图象上点的坐标特征,求出当y=1.8时x的值,由此即可得出结论;
(3)利用二次函数图象上点的坐标特征可求出抛物线与y轴交点坐标,由抛物线的形状不变可设扩建后水柱所在抛物线(第一象限部分)的函数表达式为![]() ,代入点(16,0)可求出b的值,再利用配方法将二次函数表达式变形为顶点式,即可得出结论.
,代入点(16,0)可求出b的值,再利用配方法将二次函数表达式变形为顶点式,即可得出结论.
(1)解:设水柱所在抛物线(第一象限部分)的函数表达式为![]()
将(8,0)代入![]() ,得:
,得:
25a+5=0
解得:![]()
∴水柱所在抛物线(第一象限部分)的函数表达式为![]()
(2)解:当![]() 时,有
时,有![]()
解得:![]()
∴为了不被淋湿,身高1.8米的人站立时必须在离水池中心7米以内.
(3)解:当x=0时,![]()
设扩建后水柱所在抛物线(第一象限部分)的函数表达式为![]()
∵该函数图象经过点(16,0)
∴![]()
解得:![]()
∴扩建后水柱所在抛物线(第一象限部分)的函数表达式为
![]()
∴扩建后喷水池水柱的最大高度为![]()


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
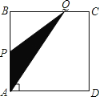
【题目】如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
A.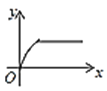 B.
B.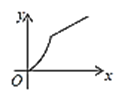 C.
C.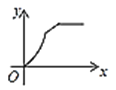 D.
D.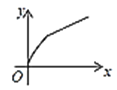
查看答案和解析>>
科目:初中数学 来源: 题型:
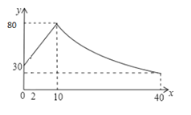
【题目】学生上课时注意力集中的程度可以用注意力指数表示.某班学生在一节数学课中的注意力指数![]() 随上课时间
随上课时间![]() (分钟)的变化图象如图.上课开始时注意力指数为30,第10分钟时注意力指数为80,前10分钟内注意力指数
(分钟)的变化图象如图.上课开始时注意力指数为30,第10分钟时注意力指数为80,前10分钟内注意力指数![]() 是时间
是时间![]() 的一次函数.10分钟以后注意力指数
的一次函数.10分钟以后注意力指数![]() 是
是![]() 的反比例函数.
的反比例函数.
(1)求出![]() 时和
时和![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果讲解一道较难的数学题要求学生的注意力指数不小于50,为了保证教学效果本节课讲完这道题不能超过多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
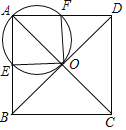
【题目】已知,如图,正方形ABCD的对角线AC,BD相交于点O,点E为AB上一点(不与A.B两点重合),过点O,A,E的⊙I交AD于F,AB=5
(1)求⊙I的直径的取值范围;
(2)若⊙I的半径为2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
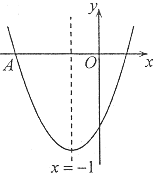
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(-3,0),其对称轴为直线x=-1,有下列结论:①abc<0;②a-b-2c>0;③关于![]() 的方程ax2+(b-m)x+c=m有两个不相等的实数根;④若
的方程ax2+(b-m)x+c=m有两个不相等的实数根;④若![]() ,
,![]() 是抛物线上两点,且
是抛物线上两点,且![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为_____.
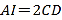
查看答案和解析>>
科目:初中数学 来源: 题型:
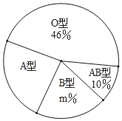
【题目】“只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、AB、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):
血型统计表
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)本次随机抽取献血者人数为 人,图中m= ;
(2)补全表中的数据;
(3)若这次活动中该校有1300人义务献血,估计大约有多少人是A型血?
(4)现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小田同学学习反比例函数![]() 的图象和性质后,对新函数
的图象和性质后,对新函数![]() 的图象和性质进行了探究,以下是她的探究过程:.
的图象和性质进行了探究,以下是她的探究过程:.
第一步:在直角坐标系中,作出函数![]() 的图象;
的图象;
第二步:通过列表、描点、连线,作出新函数![]() 的图象
的图象
①列表:
| … | -4 | -2 | -1 | 0 | 1 | 3 | 4 | 5 | 6 | … |
| … | 1 | 1.5 | 2 | 3 | 6 | -6 | -3 | -2 | -1.5 | … |
②描点:如图所示.

(1)请在图中,帮助小田同学完成连线的步骤;
(2)观察图象,发现函数![]() 与函数
与函数![]() 的图象都是双曲线,并且形状也相同,只是位置发生了改变,由此可知,函数
的图象都是双曲线,并且形状也相同,只是位置发生了改变,由此可知,函数![]() 的图象可由函数
的图象可由函数![]() 的图象平移得到,请写出函数
的图象平移得到,请写出函数![]() 的图象是怎样平移得到的?
的图象是怎样平移得到的?
(3)若点![]() ,
,![]() 在函数图象
在函数图象![]() 上,且
上,且![]() ,则
,则![]()
![]() (选填“>”“<”或“=”)
(选填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
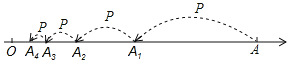
【题目】数轴上OA两点的距离为4,一动点P从A点出发按以下规律跳动:第一次跳动到AO的中点A1处,第二次从A1点跳动到A1O的中点A2处,第三次从A2跳动到A2O的中点A3处按照这样的规律,继续跳动到点A4A5A6……An(n≥3,n是整数)处那么线段A3O的长度为_________,AnA的长度为_________ 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com