
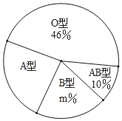
【题目】“只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、AB、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):
血型统计表
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)本次随机抽取献血者人数为 人,图中m= ;
(2)补全表中的数据;
(3)若这次活动中该校有1300人义务献血,估计大约有多少人是A型血?
(4)现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.
【答案】(1)50,20;(2)12,23;(3)312;(4)![]() .
.
【解析】
(1)用AB型的人数除以它所占的百分比得到随机抽取的献血者的总人数,然后计算m的值;
(2)先计算出O型的人数,再计算出A型人数,从而可补全上表中的数据;
(3)用样本中A型的人数除以50得到血型是A型的概率,然后用3000乘以此概率可估计这3000人中是A型血的人数;
(4)画出树状图,根据概率公式即可得到结果.
解:(1)这次随机抽取的献血者人数为5÷10%=50(人),
所以m=![]() ×100=20;
×100=20;
故答案为50,20;
(2)O型献血的人数为46%×50=23(人),
A型献血的人数为50﹣10﹣5﹣23=12(人),
血型 | A | B | AB | O |
人数 | 12 | 10 | 5 | 23 |
故答案为12,23;
(3)从献血者人群中任抽取一人,其血型是A型的概率=![]() =
=![]() ,1300×
,1300×![]() =312,估计这1300人中大约有312人是A型血;
=312,估计这1300人中大约有312人是A型血;
(4)画树状图如图所示,
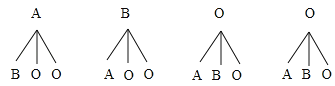
所以P(两个O型)=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求出该函数图象的顶点坐标,对称轴,图象与![]() 轴、
轴、![]() 轴的交点坐标;
轴的交点坐标;
(2)![]() 在什么范围内时,
在什么范围内时,![]() 随
随![]() 的增大而增大?当
的增大而增大?当![]() 在什么范围内时,
在什么范围内时,![]() 随
随![]() 的增大而减小?
的增大而减小?
(3)当![]() 在什么范围内时,
在什么范围内时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a<0,b,c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④3b>2c;⑤a+b>m(am+b)(m为常数,且m≠1),其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系
(1)求水柱所在抛物线(第一象限部分)的函数解析式
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿?
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度
查看答案和解析>>
科目:初中数学 来源: 题型:
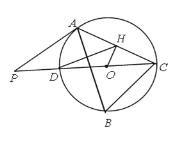
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若OH⊥AC,OH=1,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,已知正方形 ABCD,点 E 在 BC 上,点 F 在 DC 上,且∠EAF=45°,则有 BE+DF= .若 AB=4,则△CEF 的周长为 .
(2)如图 2,四边形 ABCD 中,∠BAD=∠C=90°,AB=AD,点 E,F 分别在 BC,CD 上,且∠EAF=45°,试判断 BE,EF,DF 之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,按下任意一个开关均可打开对应的一盏电灯,因刚搬进新房不久,不熟悉情况.
(1)若小明任意按下一个开关,则下列说法正确的是 .
A.小明打开的一定是楼梯灯
B.小明打开的可能是卧室灯
C.小明打开的不可能是客厅灯
D.小明打开走廊灯的概率是![]()
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.

(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离.(结果精确到1km)
(参考数据:![]() =1.73,
=1.73,![]() =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
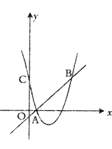
(1)求![]() 的值和抛物线的解析式;
的值和抛物线的解析式;
(2)直接写出方程![]() 的解;
的解;
(3)点![]() 是抛物线
是抛物线![]() 对称轴上的一个动点,当
对称轴上的一个动点,当![]() 的值最小时,判断
的值最小时,判断![]() 的形状.
的形状.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com