
【题目】学生上课时注意力集中的程度可以用注意力指数表示.某班学生在一节数学课中的注意力指数![]() 随上课时间
随上课时间![]() (分钟)的变化图象如图.上课开始时注意力指数为30,第10分钟时注意力指数为80,前10分钟内注意力指数
(分钟)的变化图象如图.上课开始时注意力指数为30,第10分钟时注意力指数为80,前10分钟内注意力指数![]() 是时间
是时间![]() 的一次函数.10分钟以后注意力指数
的一次函数.10分钟以后注意力指数![]() 是
是![]() 的反比例函数.
的反比例函数.
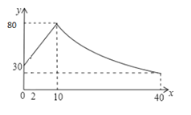
(1)求出![]() 时和
时和![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果讲解一道较难的数学题要求学生的注意力指数不小于50,为了保证教学效果本节课讲完这道题不能超过多少分钟?
 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】有一块等腰三角形白铁皮余料ABC,它的腰AB=10cm,底边BC=12cm.
(1)圆圆同学想从中裁出最大的圆,请帮他求出该圆的半径;
(2)方方同学想从中裁出最大的正方形,请帮他求出该正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求出该函数图象的顶点坐标,对称轴,图象与![]() 轴、
轴、![]() 轴的交点坐标;
轴的交点坐标;
(2)![]() 在什么范围内时,
在什么范围内时,![]() 随
随![]() 的增大而增大?当
的增大而增大?当![]() 在什么范围内时,
在什么范围内时,![]() 随
随![]() 的增大而减小?
的增大而减小?
(3)当![]() 在什么范围内时,
在什么范围内时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=﹣![]() (x+1)2﹣2
(x+1)2﹣2
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为
(2)当x 时,y随x的增大而增大
(3)怎样移动抛物线y=﹣![]() x2就可以得到抛物线y=﹣
x2就可以得到抛物线y=﹣![]() (x+1)2﹣2
(x+1)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C.D是二次函数图象上的一对对称点,一次函数的图象过点B. D.
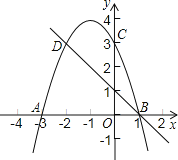
(1)求D点坐标;
(2)根据图象直接写出使一次函数值小于二次函数值的x的取值范围
(3)求二次函数的解析式及顶点坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣6mx+9m2+n(m,n为常数)
(1)若n=﹣4,这个函数图象与x轴交于A,B两点(点A,B分别在x轴的正、负半轴),与y轴交于点C,试求△ABC面积的最大值;
(2)若n=4m+4,当x轴上的动点Q到抛物线的顶点P的距离最小值为4时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a<0,b,c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④3b>2c;⑤a+b>m(am+b)(m为常数,且m≠1),其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
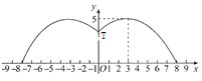
【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系
(1)求水柱所在抛物线(第一象限部分)的函数解析式
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿?
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.

(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离.(结果精确到1km)
(参考数据:![]() =1.73,
=1.73,![]() =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com