
【题目】已知函数y=﹣![]() (x+1)2﹣2
(x+1)2﹣2
(1)指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为
(2)当x 时,y随x的增大而增大
(3)怎样移动抛物线y=﹣![]() x2就可以得到抛物线y=﹣
x2就可以得到抛物线y=﹣![]() (x+1)2﹣2
(x+1)2﹣2
【答案】(1)开口方向向下、对称轴为x=-1、顶点坐标为(-1,-2);(2)![]() ;(3)向左平移1个单位长度,再向下平移2个单位长度.
;(3)向左平移1个单位长度,再向下平移2个单位长度.
【解析】
(1)利用二次根式的性质确定出开口方向,顶点坐标以及对称轴即可;
(2)由对称轴和开口方向得出增减性;
(3)根据平移规律回答问题.
(1)∵a=-![]() <0,
<0,
∴抛物线开口向下,
顶点坐标为(-1,-2),对称轴为直线x=-1;
故答案是:开口方向向下、对称轴为x=-1、顶点坐标为(-1,-2);
(2)∵对称轴x=-1,
∴当x<-1时,y随x的增大而减大.
故答案是:![]() ;
;
(3)向左平移1个单位长度,再向下平移2个单位长度移动抛物线y=-![]() x2就可以得到抛物线y=-
x2就可以得到抛物线y=-![]() (x+1)2-2.
(x+1)2-2.


科目:初中数学 来源: 题型:
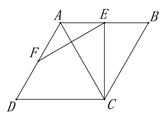
【题目】如图,四边形ABCD是边长为2的菱形,E,F分别是AB,AD的中点,连接EF,EC,将△FAE绕点F旋转180°得到△FDM.
(1)补全图形并证明:EF⊥AC;
(2)若∠B=60°,求△EMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
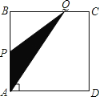
A.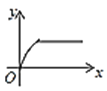 B.
B.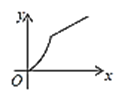 C.
C.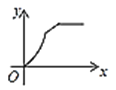 D.
D.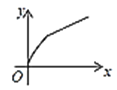
查看答案和解析>>
科目:初中数学 来源: 题型:
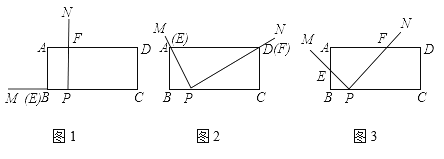
【题目】如图1,在矩形ABCD中,AB=2,BC=5,BP=1,∠MPN=90°,将∠MPN绕点P从PB处开始顺时针方向旋转,PM交边AB于点E,PN交边AD于点F,当PE旋转至PA处时,∠MPN的旋转随即停止.
(1)如图2,在旋转中发现当PM经过点A时,PN也经过点D,求证:△ABP ∽△PCD
(2)如图3,在旋转过程中,![]() 的值是否为定值?若是,请求出该定值;若不是,请说明理由
的值是否为定值?若是,请求出该定值;若不是,请说明理由
(3)设AE![]() ,连结EF,则在旋转过程中,当
,连结EF,则在旋转过程中,当![]() 为何值时,△BPE与△PEF相似.
为何值时,△BPE与△PEF相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)x2+1=3x
(2)(x﹣2)(x﹣3)=12
(3)(2x﹣3)2+x(2x﹣3)=0(因式分解法)
(4)2x2﹣4x﹣1=0(用配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润, 商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件; 若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x( 元/件)的一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生上课时注意力集中的程度可以用注意力指数表示.某班学生在一节数学课中的注意力指数![]() 随上课时间
随上课时间![]() (分钟)的变化图象如图.上课开始时注意力指数为30,第10分钟时注意力指数为80,前10分钟内注意力指数
(分钟)的变化图象如图.上课开始时注意力指数为30,第10分钟时注意力指数为80,前10分钟内注意力指数![]() 是时间
是时间![]() 的一次函数.10分钟以后注意力指数
的一次函数.10分钟以后注意力指数![]() 是
是![]() 的反比例函数.
的反比例函数.
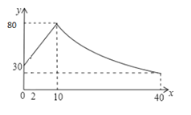
(1)求出![]() 时和
时和![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果讲解一道较难的数学题要求学生的注意力指数不小于50,为了保证教学效果本节课讲完这道题不能超过多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
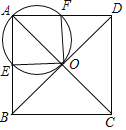
【题目】已知,如图,正方形ABCD的对角线AC,BD相交于点O,点E为AB上一点(不与A.B两点重合),过点O,A,E的⊙I交AD于F,AB=5
(1)求⊙I的直径的取值范围;
(2)若⊙I的半径为2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小田同学学习反比例函数![]() 的图象和性质后,对新函数
的图象和性质后,对新函数![]() 的图象和性质进行了探究,以下是她的探究过程:.
的图象和性质进行了探究,以下是她的探究过程:.
第一步:在直角坐标系中,作出函数![]() 的图象;
的图象;
第二步:通过列表、描点、连线,作出新函数![]() 的图象
的图象
①列表:
| … | -4 | -2 | -1 | 0 | 1 | 3 | 4 | 5 | 6 | … |
| … | 1 | 1.5 | 2 | 3 | 6 | -6 | -3 | -2 | -1.5 | … |
②描点:如图所示.

(1)请在图中,帮助小田同学完成连线的步骤;
(2)观察图象,发现函数![]() 与函数
与函数![]() 的图象都是双曲线,并且形状也相同,只是位置发生了改变,由此可知,函数
的图象都是双曲线,并且形状也相同,只是位置发生了改变,由此可知,函数![]() 的图象可由函数
的图象可由函数![]() 的图象平移得到,请写出函数
的图象平移得到,请写出函数![]() 的图象是怎样平移得到的?
的图象是怎样平移得到的?
(3)若点![]() ,
,![]() 在函数图象
在函数图象![]() 上,且
上,且![]() ,则
,则![]()
![]() (选填“>”“<”或“=”)
(选填“>”“<”或“=”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com