
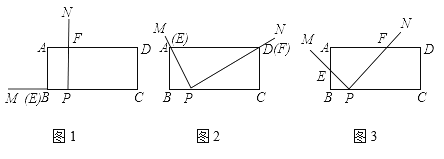
ЁОЬтФПЁПШчЭМ1ЃЌдкОиаЮABCDжаЃЌAB=2ЃЌBC=5ЃЌBP=1ЃЌЁЯMPN=90ЁуЃЌНЋЁЯMPNШЦЕуPДгPBДІПЊЪМЫГЪБеыЗНЯђа§зЊЃЌPMНЛБпABгкЕуEЃЌPNНЛБпADгкЕуFЃЌЕБPEа§зЊжСPAДІЪБЃЌЁЯMPNЕФа§зЊЫцМДЭЃжЙ.
ЃЈ1ЃЉШчЭМ2ЃЌдка§зЊжаЗЂЯжЕБPMОЙ§ЕуAЪБЃЌPNвВОЙ§ЕуDЃЌЧѓжЄЃКЁїABP ЁзЁїPCD
ЃЈ2ЃЉШчЭМ3ЃЌдка§зЊЙ§ГЬжаЃЌ![]() ЕФжЕЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГіИУЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩ
ЕФжЕЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГіИУЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩ
ЃЈ3ЃЉЩшAE![]() ЃЌСЌНсEFЃЌдђдка§зЊЙ§ГЬжаЃЌЕБ
ЃЌСЌНсEFЃЌдђдка§зЊЙ§ГЬжаЃЌЕБ![]() ЮЊКЮжЕЪБЃЌЁїBPEгыЁїPEFЯрЫЦ.
ЮЊКЮжЕЪБЃЌЁїBPEгыЁїPEFЯрЫЦ.
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ![]() ЕФжЕЪЧЖЈжЕЃЌИУЖЈжЕЮЊ
ЕФжЕЪЧЖЈжЕЃЌИУЖЈжЕЮЊ![]() ЃЛЃЈ3ЃЉЕБ
ЃЛЃЈ3ЃЉЕБ![]() Лђ
Лђ![]() ЪБЃЌЁїBPEгыЁїPEFЯрЫЦ
ЪБЃЌЁїBPEгыЁїPEFЯрЫЦ
ЁОНтЮіЁП
ЃЈ1ЃЉвђЮЊдкОиаЮжаЃЌЫљвджЛвЊдйжЄУїЁЯBAP=ЁЯCPDМДПЩЃЛЃЈ2ЃЉжЄУїБпБШЮЊЖЈжЕЃЌПМТЧЯрЫЦШ§НЧаЮЃЌЙ§ЕуFзїFGЁЭBCгкGЃЌДДдьЁїPGFВЂжЄУїЦфгыЁїEBP ЯрЫЦЃЛЃЈ3ЃЉЪЙЁїBPE ЁзЁїPFEЃЌФЧУД![]() ЃЌЫуГіmжЕЃЌЗДжЄЯрЫЦ.
ЃЌЫуГіmжЕЃЌЗДжЄЯрЫЦ.
ЃЈ1ЃЉжЄУїЃКЁпЫФБпаЮABCDЪЧОиаЮ
ЁрЁЯB=ЁЯC=90Ёу
ЁрЁЯBAP+ЁЯBPA=90Ёу
ЁпЁЯMPN=90Ёу
ЁрЁЯCPD+ЁЯBPA=90Ёу
ЁрЁЯBAP=ЁЯCPD
ЁрЁїABP ЁзЁїPCD
ЃЈ2ЃЉЙ§ЕуFзїFGЁЭBCгкG
ЁрЁЯFGP=90Ёу
ЁрЁЯFGP=ЁЯBЃЌЁЯPFG+ЁЯFPG=90Ёу
взжЊЫФБпаЮABGFЪЧОиаЮЃЌ
ЁрFG=AB=2
ЁпЁЯMPN=90Ёу
ЁрЁЯEPB+ЁЯFPG=90Ёу
ЁрЁЯEPB=ЁЯFPG
ЁрЁїEBP ЁзЁїPGF
Ёр![]()
Ёр![]() ЕФжЕЪЧЖЈжЕЃЌИУЖЈжЕЮЊ
ЕФжЕЪЧЖЈжЕЃЌИУЖЈжЕЮЊ![]()
ЃЈ3ЃЉЁпAE![]()
ЁрBE![]()
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ
ЁпЁЯB=ЁЯEPF=90Ёу
ЁрЁїBPE ЁзЁїPFE
Ёр![]()
Ёр![]()
Ёр![]()
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ
ЁпЁЯB=ЁЯEPF=90Ёу
ЁрЁїBPE ЁзЁїPEF
Ёр![]()
Ёр![]()
Ёр![]()
злЩЯЃЌЕБ![]() Лђ
Лђ![]() ЪБЃЌЁїBPEгыЁїPEFЯрЫЦ.
ЪБЃЌЁїBPEгыЁїPEFЯрЫЦ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпMNгыxжсЃЌyжсЗжБ№ЯрНЛгкAЃЌCСНЕуЃЌЗжБ№Й§AЃЌCСНЕузїxжсЃЌyжсЕФДЙЯпЯрНЛгкBЕуЃЌЧвOAЃЌOCЃЈOAЃОOCЃЉЕФГЄЗжБ№ЪЧвЛдЊЖўДЮЗНГЬx2Љ14x+48=0ЕФСНИіЪЕЪ§ИљЃЎ

ЃЈ1ЃЉЧѓCЕузјБъЃЛ
ЃЈ2ЃЉЧѓжБЯпMNЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкжБЯпMNЩЯДцдкЕуPЃЌЪЙвдЕуPЃЌBЃЌCШ§ЕуЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧыжБНгаДГіPЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
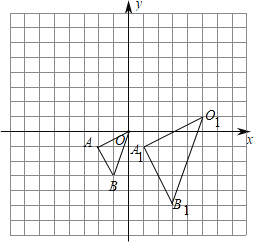
ЁОЬтФПЁПдкШчЭМЫљЪОЕФЗНИёжаЃЌЁїOABЕФЖЅЕузјБъЗжБ№ЮЊOЃЈ0ЃЌ0ЃЉЁЂAЃЈЉ2ЃЌЉ1ЃЉЃЌBЃЈЉ1ЃЌЉ3ЃЉЃЌЁїO1A1B1гыЁїOABЪЧЙигкЕуPЮЊЮЛЫЦжааФЕФЮЛЫЦЭМаЮЃЎ
ЃЈ1ЃЉдкЭМжаБъГіЮЛЫЦжааФPЕФЮЛжУЃЌВЂаДГіЕуPЕФзјБъМАЁїO1A1B1гыЁїOABЕФЯрЫЦБШЃЛ
ЃЈ2ЃЉвддЕуOЮЊЮЛЫЦжааФЃЌдкyжсЕФзѓВрЛГіЁїOABЕФСэвЛИіЮЛЫЦЁїOA2B2ЃЌЪЙЫќгыЁїOABЕФЯрЫЦБШЮЊ2ЃК1ЃЌВЂаДГіЕуBЕФЖдгІЕуB2ЕФзјБъЃЎ
ЃЈ3ЃЉЁїOA2B2ЕФУцЛ§ЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() гыxжсжЛгавЛИіНЛЕуЃЌЧвНЛЕуЮЊAЃЈ-2,0ЃЉ.
гыxжсжЛгавЛИіНЛЕуЃЌЧвНЛЕуЮЊAЃЈ-2,0ЃЉ.
ЃЈ1ЃЉЧѓbЃЌcЕФжЕЃЛ
ЃЈ2ЃЉШєХзЮяЯпгыyжсЕФНЛЕуЮЊBЃЌзјБъдЕуЮЊOЃЌЧѓЁїOABЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓГіИУКЏЪ§ЭМЯѓЕФЖЅЕузјБъЃЌЖдГЦжсЃЌЭМЯѓгы![]() жсЁЂ
жсЁЂ![]() жсЕФНЛЕузјБъЃЛ
жсЕФНЛЕузјБъЃЛ
ЃЈ2ЃЉ![]() дкЪВУДЗЖЮЇФкЪБЃЌ
дкЪВУДЗЖЮЇФкЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓЃПЕБ
ЕФдіДѓЖјдіДѓЃПЕБ![]() дкЪВУДЗЖЮЇФкЪБЃЌ
дкЪВУДЗЖЮЇФкЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁЃП
ЕФдіДѓЖјМѕаЁЃП
ЃЈ3ЃЉЕБ![]() дкЪВУДЗЖЮЇФкЪБЃЌ
дкЪВУДЗЖЮЇФкЪБЃЌ![]() ЃП
ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌBDЮЊвЛЬѕЖдНЧЯпЃЌADЁЮBCЃЌADЃН2BCЃЌЁЯABDЃН90ЁуЃЌEЮЊADЕФжаЕуЃЌСЌНгBEЃЎ
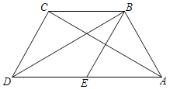
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮBCDEЮЊСтаЮЃЛ
ЃЈ2ЃЉСЌНгACЃЌШєACЦНЗжЁЯBADЃЌABЃН2ЃЌЧѓСтаЮBCDEЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§y=Љ![]() ЃЈx+1ЃЉ2Љ2
ЃЈx+1ЃЉ2Љ2
ЃЈ1ЃЉжИГіКЏЪ§ЭМЯѓЕФПЊПкЗНЯђЪЧЁЁ ЁЁЃЌЖдГЦжсЪЧЁЁ ЁЁЃЌЖЅЕузјБъЮЊЁЁ ЁЁ
ЃЈ2ЃЉЕБxЁЁ ЁЁЪБЃЌyЫцxЕФдіДѓЖјдіДѓ
ЃЈ3ЃЉдѕбљвЦЖЏХзЮяЯпy=Љ![]() x2ОЭПЩвдЕУЕНХзЮяЯпy=Љ
x2ОЭПЩвдЕУЕНХзЮяЯпy=Љ![]() ЃЈx+1ЃЉ2Љ2
ЃЈx+1ЃЉ2Љ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНx2Љ6mx+9m2+nЃЈmЃЌnЮЊГЃЪ§ЃЉ
ЃЈ1ЃЉШєnЃНЉ4ЃЌетИіКЏЪ§ЭМЯѓгыxжсНЛгкAЃЌBСНЕуЃЈЕуAЃЌBЗжБ№дкxжсЕФе§ЁЂИКАыжсЃЉЃЌгыyжсНЛгкЕуCЃЌЪдЧѓЁїABCУцЛ§ЕФзюДѓжЕЃЛ
ЃЈ2ЃЉШєnЃН4m+4ЃЌЕБxжсЩЯЕФЖЏЕуQЕНХзЮяЯпЕФЖЅЕуPЕФОрРызюаЁжЕЮЊ4ЪБЃЌЧѓЕуQЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ 1ЃЌвбжЊе§ЗНаЮ ABCDЃЌЕу E дк BC ЩЯЃЌЕу F дк DC ЩЯЃЌЧвЁЯEAF=45ЁуЃЌдђга BE+DF= .Шє AB=4ЃЌдђЁїCEF ЕФжмГЄЮЊ .
ЃЈ2ЃЉШчЭМ 2ЃЌЫФБпаЮ ABCD жаЃЌЁЯBAD=ЁЯC=90ЁуЃЌAB=ADЃЌЕу EЃЌF ЗжБ№дк BCЃЌCD ЩЯЃЌЧвЁЯEAF=45ЁуЃЌЪдХаЖЯ BEЃЌEFЃЌDF жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com