
【题目】如图,二次函数的图象与x轴相交于A(3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C.D是二次函数图象上的一对对称点,一次函数的图象过点B. D.
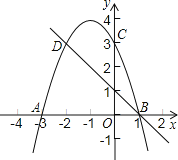
(1)求D点坐标;
(2)根据图象直接写出使一次函数值小于二次函数值的x的取值范围
(3)求二次函数的解析式及顶点坐标;
【答案】(1)D(-2,3);(2)-2<x<1;(3)y=-x2-2x+3,(-1,4).
【解析】
(1)先求出二次函数的对称轴,然后根据抛物线的对称性来求点D的坐标;
(2)根据图象直接写出答案;
(3)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c常数),把点A、B、C的坐标分别代入函数解析式,列出关于系数a、b、c的方程组求解即可.
解:(1)∵如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,
∴对称轴是x=![]() =-1.
=-1.
又点C(0,3),点C、D是二次函数图象上的一对对称点,
∴D(-2,3);
(2)由图像可知,一次函数值小于二次函数值的x的取值范围是-2<x<1;
(3)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c常数),
根据题意得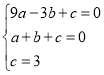 ,
,
解得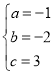 ,
,
∴二次函数的解析式为y=-x2-2x+3=-(x+1)2+4,
∴顶点坐标(-1,4).


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=x与双曲线y=![]() (k≠0)的一个交点为P(
(k≠0)的一个交点为P(![]() ,n).将直线向上平移b(0>0)个单位长度后,与x轴,y轴分别交于点A,点B,与双曲线的一个交点为Q.若AQ=3AB,则b=____.
,n).将直线向上平移b(0>0)个单位长度后,与x轴,y轴分别交于点A,点B,与双曲线的一个交点为Q.若AQ=3AB,则b=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位数n,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称n为“极数”。
(1)请任意写出三个“极数”;并猜想任意一个“极数”是否是99的倍数,请说明理由;
(2)如果一个正整数a是另一个正整数b的平方,则称正整数a是完全平方数。若四位数m为“极数”,记D(m)=![]() ,求满足D(m)是完全平方数的所有m.
,求满足D(m)是完全平方数的所有m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)x2+1=3x
(2)(x﹣2)(x﹣3)=12
(3)(2x﹣3)2+x(2x﹣3)=0(因式分解法)
(4)2x2﹣4x﹣1=0(用配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】施秉县城关镇为打造“绿色小镇”,投入资金进行河道治污.已知2017年投入资金1000万元,2019年投入资金1210万元.
(1)求该镇投入资金从2017年至2019年的年平均增长率;
(2)若2020年投入资金保持前两年的年平均增长率不变,求该镇2020年预计投入资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生上课时注意力集中的程度可以用注意力指数表示.某班学生在一节数学课中的注意力指数![]() 随上课时间
随上课时间![]() (分钟)的变化图象如图.上课开始时注意力指数为30,第10分钟时注意力指数为80,前10分钟内注意力指数
(分钟)的变化图象如图.上课开始时注意力指数为30,第10分钟时注意力指数为80,前10分钟内注意力指数![]() 是时间
是时间![]() 的一次函数.10分钟以后注意力指数
的一次函数.10分钟以后注意力指数![]() 是
是![]() 的反比例函数.
的反比例函数.
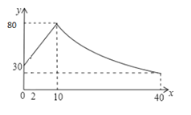
(1)求出![]() 时和
时和![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果讲解一道较难的数学题要求学生的注意力指数不小于50,为了保证教学效果本节课讲完这道题不能超过多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若实数a,b满足a+b=1时,就称点P(a,b)为“平衡点”.
(1)判断点A(3,﹣4)、B(![]() -1,2-
-1,2-![]() )是不是平衡点;
)是不是平衡点;
(2)已知抛物线y=![]() x2+(p﹣t﹣1)x+q+t﹣3(t>3)上有且只有一个“平衡点”,且当﹣2≤p≤3时,q的最小值为t,求t的值.
x2+(p﹣t﹣1)x+q+t﹣3(t>3)上有且只有一个“平衡点”,且当﹣2≤p≤3时,q的最小值为t,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
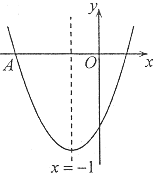
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(-3,0),其对称轴为直线x=-1,有下列结论:①abc<0;②a-b-2c>0;③关于![]() 的方程ax2+(b-m)x+c=m有两个不相等的实数根;④若
的方程ax2+(b-m)x+c=m有两个不相等的实数根;④若![]() ,
,![]() 是抛物线上两点,且
是抛物线上两点,且![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com