
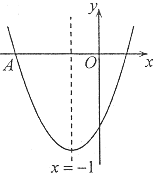
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(-3,0),其对称轴为直线x=-1,有下列结论:①abc<0;②a-b-2c>0;③关于![]() 的方程ax2+(b-m)x+c=m有两个不相等的实数根;④若
的方程ax2+(b-m)x+c=m有两个不相等的实数根;④若![]() ,
,![]() 是抛物线上两点,且
是抛物线上两点,且![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据抛物线开口方向、对称轴、及与y轴的交点位置可对①进行判断;根据对称轴和抛物线与x的一个交点(-3,0)可得另一个交点坐标为(1,0),可知![]() =-3,即c=-3a,根据对称轴方程可得b=2a,代入a-b-2c,根据a的符号即可对②进行判断;根据b2-4ac>0,b=2a,判断方程ax2+(b-m)x+c=m的判别式的符号即可对③进行判断;把P、Q两点坐标代入抛物线解析式,根据y1>y2列出不等式,根据c=-3a,b=2a解不等式求出m的取值范围即可对④进行判断.
=-3,即c=-3a,根据对称轴方程可得b=2a,代入a-b-2c,根据a的符号即可对②进行判断;根据b2-4ac>0,b=2a,判断方程ax2+(b-m)x+c=m的判别式的符号即可对③进行判断;把P、Q两点坐标代入抛物线解析式,根据y1>y2列出不等式,根据c=-3a,b=2a解不等式求出m的取值范围即可对④进行判断.
∵抛物线开口向上,与y轴交点在y轴负半轴,
∴a>0,c<0,
∵对称轴x=![]() =-1<0,
=-1<0,
∴b>0,b=2a,
∴abc<0,故①正确,
∵对称轴为x=-1,与x轴的一个交点为A(-3,0),
∴抛物线与x轴的另一个交点为(1,0),
∴![]() =-3,即c=-3a,
=-3,即c=-3a,
∴a-b-2c=a-2a+6a=5a>0,故②正确,
方程ax2+(b-m)x+c=m的判别式为△=(b-m)2-4a(c-m)=b2-4ac+m2-2m(b-2a)
∵抛物线y=ax2+bx+c与x轴有两个交点,
∴b2-4ac>0,
∵b=2a,
∴△= b2-4ac+m2>0,
∴方程ax2+(b-m)x+c=m有两个不相等的实数根,故③正确,
∵P(-5,y1)、Q(m,y2)是抛物线上两点,
∴y1=25a-5b+c,y2=am2+bm+c,
∵y1>y2,
∴25a-5b>am2+bm,
∵b=2a,
∴25a-10a>am2+2am,
∵a>0,
∴m2+2m-15<0,
解得:-5<m<3,故④正确,
综上所述:正确的结论有①②③④,共4个,
故选D.


科目:初中数学 来源: 题型:
【题目】有一个二次函数满足以下条件:
①函数图象与x轴的交点坐标分别为A(1,0),B(x2,y2)(点B在点A的右侧);
②对称轴是x=3;
③该函数有最小值是﹣2.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象x>x2的部分图象向下翻折与原图象未翻折的部分组成图象“G”,平行于x轴的直线与图象“G”相交于点C(x3,y3)、D(x4,y4)、E(x5,y5)(x3<x4<x5),结合画出的函数图象求x3+x4+x5的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C.D是二次函数图象上的一对对称点,一次函数的图象过点B. D.
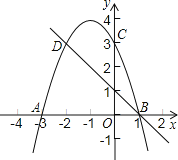
(1)求D点坐标;
(2)根据图象直接写出使一次函数值小于二次函数值的x的取值范围
(3)求二次函数的解析式及顶点坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a<0,b,c为常数)的图象如图所示,下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④3b>2c;⑤a+b>m(am+b)(m为常数,且m≠1),其中正确的结论有_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
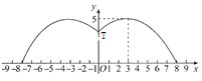
【题目】有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的立杆上点T处汇合.如图所示为截面图,以水平方向为x轴,喷水池中心为原点建立直角坐标系
(1)求水柱所在抛物线(第一象限部分)的函数解析式
(2)正在喷水时,身高1.8米的人,应站在离水池中心多远的地方就能不被淋湿?
(3)在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心的立杆上点T处汇合,请探究扩建后喷水池水柱的最大高度
查看答案和解析>>
科目:初中数学 来源: 题型:
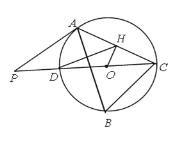
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若OH⊥AC,OH=1,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,按下任意一个开关均可打开对应的一盏电灯,因刚搬进新房不久,不熟悉情况.
(1)若小明任意按下一个开关,则下列说法正确的是 .
A.小明打开的一定是楼梯灯
B.小明打开的可能是卧室灯
C.小明打开的不可能是客厅灯
D.小明打开走廊灯的概率是![]()
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com