
【题目】二次函数![]() (
(![]() )的图象如图所示,分析下列四个结论:①
)的图象如图所示,分析下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )
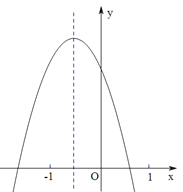
A.1个B.2个C.3个D.4个
【答案】B
【解析】
①由二次函数图象的开口方向、对称轴在y轴左侧以及与y轴交于正半轴,即可得出a<0,![]() <0,c>0,进而可得出abc>0,结论①错误;②由二次函数图象与x轴有两个交点,即可得出b2-4ac>0,结论②正确;③由
<0,c>0,进而可得出abc>0,结论①错误;②由二次函数图象与x轴有两个交点,即可得出b2-4ac>0,结论②正确;③由![]() >-1,a<0,可得出b>2a,即b-2a>0,结论③错误;④由当x=1时y<0和当x=-1时y>0,可得出a+b+c<0,a-b+c>0,两式相乘后即可得出(a+c)2-b2<0,即(a+c)2<b2,结论④正确.综上即可得出结论.
>-1,a<0,可得出b>2a,即b-2a>0,结论③错误;④由当x=1时y<0和当x=-1时y>0,可得出a+b+c<0,a-b+c>0,两式相乘后即可得出(a+c)2-b2<0,即(a+c)2<b2,结论④正确.综上即可得出结论.
解:①∵二次函数图象开口向下,对称轴在y轴左侧,与y轴交于正半轴,
∴a<0,![]() <0,c>0,
<0,c>0,
∴b<0,
∴abc>0,结论①错误;
②∵二次函数图象与x轴有两个交点,
∴b2-4ac>0,结论②正确;
③∵![]() >-1,a<0,
>-1,a<0,
∴b>2a,
∴b-2a>0,结论③错误;
④∵当x=1时,y<0;当x=-1时,y>0,
∴a+b+c<0,a-b+c>0,
∴(a+b+c)(a-b+c)<0,
∴(a+c)2-b2<0,即(a+c)2<b2,结论④正确.
故选择:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动(抛物线随顶点一起平移),与
上运动(抛物线随顶点一起平移),与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),点
的左侧),点![]() 的横坐标最小值为-6,则点
的横坐标最小值为-6,则点![]() 的横坐标最大值为( )
的横坐标最大值为( )
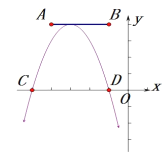
A.-3B.1C.5D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,函数y=![]() 的图像与x、y轴分别交于点A、B.以AB为直径作
的图像与x、y轴分别交于点A、B.以AB为直径作![]() M.
M.
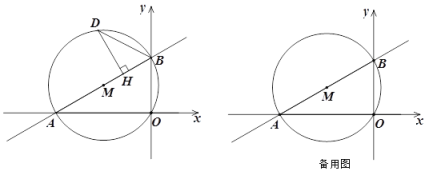
(1)求AB的长;
(2)点D是![]() M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
①当△BDH中有一个角等于![]() BAO两倍时,求点D的坐标;
BAO两倍时,求点D的坐标;
②当![]() DBH=45°时,求点D的坐标.
DBH=45°时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
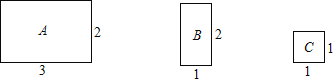
(1)搅匀后从中摸出1个盒子,求摸出的盒子中是![]() 型矩形纸片的概率;
型矩形纸片的概率;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).
查看答案和解析>>
科目:初中数学 来源: 题型:
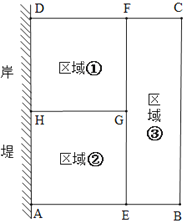
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且AE:BE=2:1.设BC的长度是![]() 米,矩形区域ABCD的面积为
米,矩形区域ABCD的面积为![]() 平方米.
平方米.
(1)求![]() 与
与![]() 之间的函数关系式,并注明自变量
之间的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)![]() 取何值时,
取何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、C的坐标分别为(0,8)、(6,0),以AC为直径作⊙O,交坐标轴于点B,点D是⊙O 上一点,且![]() ,过点D作DE⊥BC,垂足为E.
,过点D作DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)求线段CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
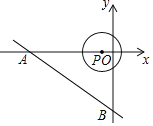
【题目】如图,直线y=-![]() x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com