
【题目】如图,平面直角坐标系中,函数y=![]() 的图像与x、y轴分别交于点A、B.以AB为直径作
的图像与x、y轴分别交于点A、B.以AB为直径作![]() M.
M.
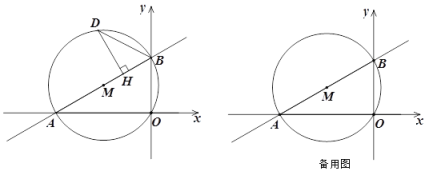
(1)求AB的长;
(2)点D是![]() M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
①当△BDH中有一个角等于![]() BAO两倍时,求点D的坐标;
BAO两倍时,求点D的坐标;
②当![]() DBH=45°时,求点D的坐标.
DBH=45°时,求点D的坐标.
【答案】(1)AB=4;(2)①(![]() ,3);D(-2
,3);D(-2![]() );②D(
);②D(![]() ).
).
【解析】
(1)根据一次函数的解析式求出A,B两点的坐标,再利用勾股定理即可求出AB的长;(2)①连接OM,由OM为Rt△AOB斜边AB上中线,证得△OBM为等边三角形,则∠OBM=60°,得到∠BAO=30°,再分∠DBH=2∠BAO=60°时与∠BDH=2∠BAO=60°时两种情况分别讨论求解;②当∠DBH=45°时,易得∠DAB=45°,则AH=DH=BH,所以M、H重合,作DC⊥y轴于C,DE⊥x轴于E,易证△DCB≌△DEA,得CB=AE,设CB=AE=a,则DC=OE=2![]() ,因为BD=
,因为BD=![]() ,由勾股定理得,DC2+CB2=DB2,所以
,由勾股定理得,DC2+CB2=DB2,所以![]() ,求出a的值,再根据题意舍去一个,即可求解.
,求出a的值,再根据题意舍去一个,即可求解.
解:(1)对于y=![]() ,
,
当x=0时,y=2;当y=0时,x=-2![]() .
.
所以点A(-2![]() ,B(0,2),
,B(0,2),
所以OB=2,OA=2![]() .根据勾股定理得,AB=
.根据勾股定理得,AB=![]() =4.
=4.
(2)①连接OM.
因为OM为Rt△AOB斜边AB上中线,
所以OM=AM=BM=![]() AB=2=OB,
AB=2=OB,
所以△OBM为等边三角形,则∠OBM=60°,
故∠BAO=30°.
1)如图,当∠DBH=2∠BAO=60°时,
连接DM,并延长交AO于点N.
∵∠DBH=60°,DM=BM,
∴△BDM为等边三角形,
∴∠DMB =60°,
故∠AMN=∠DMB =60°,
所以∠MNA=180-30°-60°=90°,
所以MN⊥AO,即DN⊥AO,
∴ON=![]() AO=
AO=![]()
DN=DM+MN=BM+![]() AM=
AM=![]() AB+
AB+![]() AB=3,
AB=3,
所以D(![]() ,3);
,3);

2)如图,

当∠BDH=2∠BAO=60°时,
∵DM=BM=AM=OM,
∴四边形BDAO为矩形,
可得,DA=BO=2,BD=OA=2![]() .
.
所以D(-2![]() ).
).
②如图,
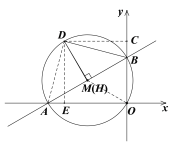
当∠DBH=45°时,
∵AH=BH,DM⊥AB,∴△ABD为等腰直角三角形,
∴∠DAB=45°,
则AH=DH=BH,所以M、H重合.
作DC⊥y轴于C,DE⊥x轴于E,
∵DE⊥AO,DC⊥CO,
∴∠ADE+∠EDB=90°,又∠EDB+∠BDC=90°,
∴∠ADE=∠BDC
又AD=BD,
∴△DCB≌△DEA(AAS),得CB=AE,
设CB=AE=a,则DC=OE=2![]() ,
,
因为BD=![]() ,
,
由勾股定理得,DC2+CB2=DB2,
所以![]() ,
,
解得a=![]() ,
,
当a=![]() 时,OC=DE=3+
时,OC=DE=3+![]() >4,不符合题意.
>4,不符合题意.
当a=![]() 时,OC=OE=
时,OC=OE=![]() ,所以D(
,所以D(![]() )
)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
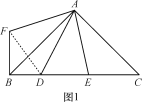
【题目】(1)如图1,△ABC中,∠BAC=90°,AB=AC,D,E在BC上,∠DAE=45°,为了探究BD,DE,CE之间的等量关系,现将△AEC绕A顺时针旋转90°后成△AFB,连接DF,经探究,你所得到的BD,DE,CE之间的等量关系式是 ;(无须证明)
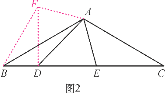
(2)如图2,在△ABC中,∠BAC=120°,AB=AC,D,E在BC上,∠DAE=60°,∠ADE=45°,试仿照(1)的方法,利用图形的旋转变换,探究BD,DE,CE之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为实数)
为实数)
(1)当![]() 时,若
时,若![]() = ,则此函数是一次函数;
= ,则此函数是一次函数;
(2)若它是一个二次函数,假设![]() ,那么:
,那么:
①当![]() 时,
时,![]() 随
随![]() 的增大而减小,请判断这个命题的真假并说明理由;
的增大而减小,请判断这个命题的真假并说明理由;
②它一定经过哪个点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学课外兴趣小组成员在研究下面三个有联系的问题,请你帮助他们解决:
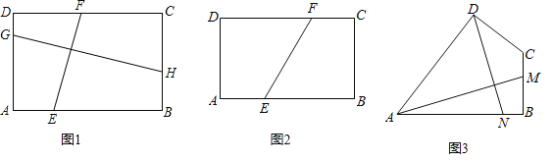
(1)如图1,矩形ABCD中,AB=a,BC=b,点E,F分别在AB,DC上,点G,H分别在AD,BC上且EF⊥GH,求![]() 的值.
的值.
(2)如图2,矩形ABCD中,AB=4,BC=3,将矩形对折,使得B、D重叠,折痕为EF,求EF的长.
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=8,BC=CD=4,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
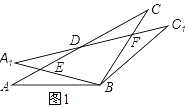
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
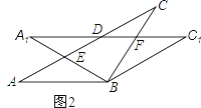
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
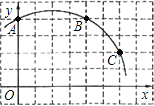
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为________.
(2)连接AD、CD,求⊙D的半径及![]() 的长;
的长;
(3)有一点E(6,0),判断点E与⊙D的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com