
【题目】已知函数![]() ,
,![]() 为实数)
为实数)
(1)当![]() 时,若
时,若![]() = ,则此函数是一次函数;
= ,则此函数是一次函数;
(2)若它是一个二次函数,假设![]() ,那么:
,那么:
①当![]() 时,
时,![]() 随
随![]() 的增大而减小,请判断这个命题的真假并说明理由;
的增大而减小,请判断这个命题的真假并说明理由;
②它一定经过哪个点?请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
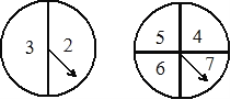
【题目】红和小华都想去参加学校组织的演讲比赛,但现在名额只有一个,于是小英想出了一个办法:让小红和小华分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被四等分),在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则小红去;若指针所指的两个数字之和为奇数,则小华去,你认为这个方法公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
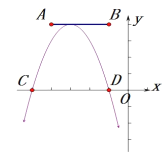
【题目】如图,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动(抛物线随顶点一起平移),与
上运动(抛物线随顶点一起平移),与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),点
的左侧),点![]() 的横坐标最小值为-6,则点
的横坐标最小值为-6,则点![]() 的横坐标最大值为( )
的横坐标最大值为( )
A.-3B.1C.5D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
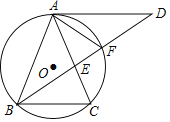
【题目】如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)求∠DAF的度数;
(2)求证:AE2=EFED;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,函数y=![]() 的图像与x、y轴分别交于点A、B.以AB为直径作
的图像与x、y轴分别交于点A、B.以AB为直径作![]() M.
M.
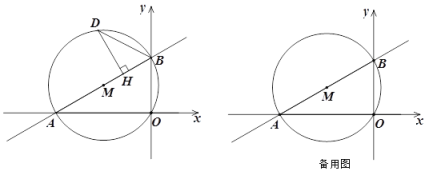
(1)求AB的长;
(2)点D是![]() M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
M上任意一点,且点D在直线AB上方,过点D作DH⊥AB,垂足为H,连接BD.
①当△BDH中有一个角等于![]() BAO两倍时,求点D的坐标;
BAO两倍时,求点D的坐标;
②当![]() DBH=45°时,求点D的坐标.
DBH=45°时,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
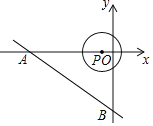
【题目】如图,直线y=-![]() x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com