
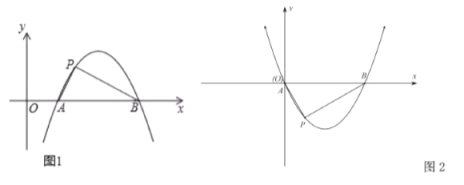
【题目】定义:如图1,抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在该抛物线上(
在该抛物线上(![]() 点与
点与![]() ,
,![]() 两点不重合),如果
两点不重合),如果![]() 的三边满足
的三边满足![]() ,则称点
,则称点![]() 为抛物线
为抛物线![]() (
(![]() )的勾股点.
)的勾股点.
(1)求证:点![]() 是抛物线
是抛物线![]() 的勾股点.
的勾股点.
(2)如图2,已知抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 的勾股点,求抛物线
的勾股点,求抛物线![]() 的函数表达式.
的函数表达式.
【答案】(1)见解析;(2)y=![]()
【解析】
(1)先解方程x2-1=0得抛物线与x轴的交点A、B的坐标为(-1,0),B(1,0),利用两点间的距离公式可得到AM2=2,BM2=2,AB2=22=4,则AM2+BM2=AB2,根据题中定义可判断点M(0,-1)是抛物线y=x2-1的勾股点;
(2)作PH⊥AB于H,如图2,先利用P点坐标求出∠PAH=60°,再根据点P(1,![]() )是抛物线C的勾股点得到∠APB=90°,所以∠PBA=30°,然后计算出BH得到B点坐标,于是可利用待定系数法求抛物线C的解析式.
)是抛物线C的勾股点得到∠APB=90°,所以∠PBA=30°,然后计算出BH得到B点坐标,于是可利用待定系数法求抛物线C的解析式.
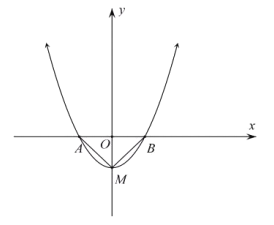
(1)如图所示:令![]() 得,
得,![]() ,解得
,解得![]()
∴![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,![]()
∴![]()
![]()
![]()
∴![]()
∴点![]() 是抛物线
是抛物线![]() 的勾股点.
的勾股点.
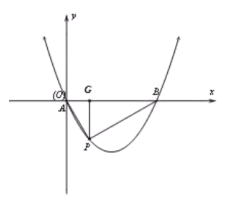
(2)抛物线![]() 过原点,即点
过原点,即点![]()
如图,作![]() 轴于点
轴于点![]()
∵点![]() 的坐标为
的坐标为![]()
∴![]() ,
,![]() ,
,![]()
∵点![]() 是抛物线
是抛物线![]() 的勾股点
的勾股点
∴![]()
∴![]() 是直角三角形
是直角三角形
设![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴点![]() 坐标为
坐标为![]()
设![]()
将点![]() 代入得:
代入得:![]()
∴![]()


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点B,与直线y=x交于点C.
x+2与x轴交于点A,与y轴交于点B,与直线y=x交于点C.

(1)求A,B,C三点的坐标;
(2)求△AOC的面积;
(3)已知点P是x轴正半轴上的一点,若△COP是等腰三角形,直接写点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
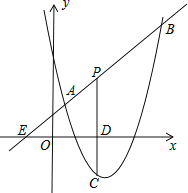
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() )和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)当C为抛物线顶点的时候,求![]() 的面积.
的面积.
(3)是否存在质疑的点P,使![]() 的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.
的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
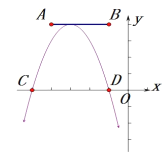
【题目】如图,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动(抛物线随顶点一起平移),与
上运动(抛物线随顶点一起平移),与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),点
的左侧),点![]() 的横坐标最小值为-6,则点
的横坐标最小值为-6,则点![]() 的横坐标最大值为( )
的横坐标最大值为( )
A.-3B.1C.5D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
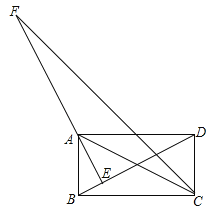
【题目】如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=![]() ;④AF=
;④AF=![]() ,其中正确结论的个数有( )
,其中正确结论的个数有( )
A.1个B.2个C.3个D.4个32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
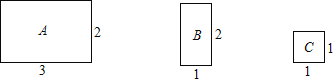
(1)搅匀后从中摸出1个盒子,求摸出的盒子中是![]() 型矩形纸片的概率;
型矩形纸片的概率;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com