
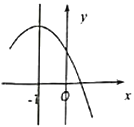
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且过点
,且过点![]() ,有下列结论:
,有下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ,其中正确的结论有( )
,其中正确的结论有( )
A.①③⑤B.①②⑤C.①④⑤D.③④⑤
【答案】A
【解析】
根据抛物线的开口方向、对称轴、与y轴的交点判定系数符号,及运用一些特殊点解答问题.
由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
直线x=1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以![]() =1,可得b=2a,
=1,可得b=2a,
a2b+4c=a4a+c=3a+c,
∵a<0,
∴3a>0,
又∵c>0
∴3a+c>0,
即a2b+4c>0,故②错误;
∵抛物线y=ax2+bx+c的对称轴是x=1.且过点(![]() ,0),
,0),
∴抛物线与x轴的另一个交点坐标为![]() ,
,
当x=![]() 时,y=0,即
时,y=0,即![]() ,
,
整理得:25a10b+4c=0,故③正确;
∵b=2a,a+b+c<0,
∴![]() b+b+c<0,
b+b+c<0,
即3b+2c<0,故④错误;
∵x=1时,函数值最大,
∴ab+c≥m2amb+c,
∴ab≥m(amb),所以⑤正确;
正确答案为:①③⑤三个.
故选C.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且BF=DE,连接AE,AF,EF.

(1)判断△ABF与△ADE有怎样的关系,并说明理由;
(2)求∠EAF的度数,写出△ABF可以由△ADE经过怎样的图形变换得到;
(3)若BC=6,DE=2,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,O为坐标原点,A(-5,8),B(3,0).
(1)如图1,求∠ABO的度数;
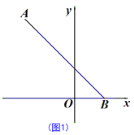
(2)如图2,点C在y轴的负半轴上,△BOC的面积为![]() ,过点C作CD∥AB交x轴于点D,点P为直线CD上一点,求△PAB的面积;
,过点C作CD∥AB交x轴于点D,点P为直线CD上一点,求△PAB的面积;
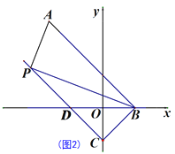
(3)如图3,在(2)的条件下,当P在第二象限时,过点P作AB的垂线交x轴于点E,点F为x轴上一点,连接PF,点G为EP延长线上一点,连接OG,若OG=FP,∠EFP+∠PGO=45°,EF=11,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+x+2交x轴于点A.B(A在B的右侧),与y轴交于点C,D为第一象限抛物线上的动点,则△ACD面积的最大值是_____
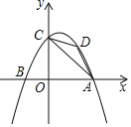
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图
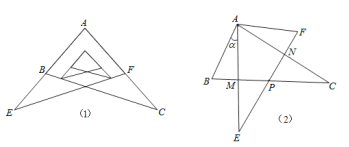
(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠BAC=90°,AB=AC,D,E在BC上,∠DAE=45°,为了探究BD,DE,CE之间的等量关系,现将△AEC绕A顺时针旋转90°后成△AFB,连接DF,经探究,你所得到的BD,DE,CE之间的等量关系式是 ;(无须证明)
(2)如图2,在△ABC中,∠BAC=120°,AB=AC,D,E在BC上,∠DAE=60°,∠ADE=45°,试仿照(1)的方法,利用图形的旋转变换,探究BD,DE,CE之间的等量关系,并证明你的结论.
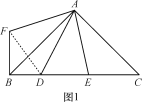
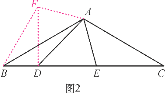
查看答案和解析>>
科目:初中数学 来源: 题型:
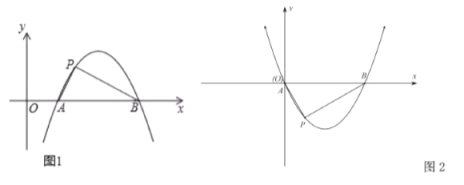
【题目】定义:如图1,抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在该抛物线上(
在该抛物线上(![]() 点与
点与![]() ,
,![]() 两点不重合),如果
两点不重合),如果![]() 的三边满足
的三边满足![]() ,则称点
,则称点![]() 为抛物线
为抛物线![]() (
(![]() )的勾股点.
)的勾股点.
(1)求证:点![]() 是抛物线
是抛物线![]() 的勾股点.
的勾股点.
(2)如图2,已知抛物线![]() (
(![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 的勾股点,求抛物线
的勾股点,求抛物线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;②3b+c+6=0;③当x2+bx+c>![]() 时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
时,x>2;④当1<x<3时,x2+(b﹣1)x+c<0,其中正确的序号是( )
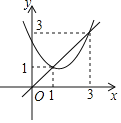
A. ①②④B. ②③④C. ②④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
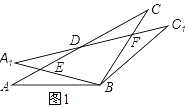
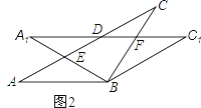
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com