
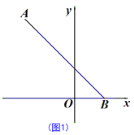
【题目】已知:在平面直角坐标系中,O为坐标原点,A(-5,8),B(3,0).
(1)如图1,求∠ABO的度数;
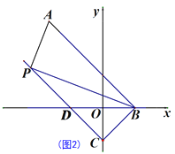
(2)如图2,点C在y轴的负半轴上,△BOC的面积为![]() ,过点C作CD∥AB交x轴于点D,点P为直线CD上一点,求△PAB的面积;
,过点C作CD∥AB交x轴于点D,点P为直线CD上一点,求△PAB的面积;
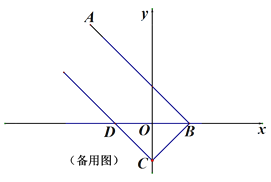
(3)如图3,在(2)的条件下,当P在第二象限时,过点P作AB的垂线交x轴于点E,点F为x轴上一点,连接PF,点G为EP延长线上一点,连接OG,若OG=FP,∠EFP+∠PGO=45°,EF=11,求点P的坐标.

【答案】(1)45°;(2)24;(3)P(-5,2)或(-7,4)
【解析】
(1)过点A作AD⊥x轴交于点D,求出AD、BD的长度即能得到答案;
(2)根据平行线间的距离处处相等,即能知道△PAB以AB为底时,高就是BC的长度,求出线段的长度,代入面积公式就能求出;
(3)分为点F在点E左侧和右侧进行讨论,根据题(2)求出PC的解析式,以及由∠EFP+∠PGO=45°推出△PFE≌△GOH,就能知道EF、OH与EO之间的关系,由EF=11,求出ED的长度后就能求出点P的横坐标,代入PC的解析式,就能求出点P的坐标.
解:(1)如图1,过点A作AD⊥x轴交于点D,
∵A(-5,8),B(3,0),
∴AD=8,BD=8,
∴△ADB是等腰直角三角形,
∴∠ABO=45°.
(2)由(1)可知,根据勾股定理可得:AB=![]() ,
,
∵△BOC的面积为![]() ,OB=3,
,OB=3,
∴ ![]() ,
,
![]() ,
,
∵点C在y轴的负半轴上,
∴C点坐标为(0,-3),
∴△BOC是等腰直角三角形,
∴∠OBC=45°,BC=![]() ,
,
∴∠ABC=∠OBC+∠ABO= 90°,
∴BC⊥AB.
∵CD∥AB,
∴点P到直线AB的距离就是BC的长度,
∴![]()
![]()
![]()
∴△PAB的面积为24.
(3)∵点G为EP延长线上一点,∠EFP+∠PGO=45°,当点G在第二象限时,∠PGO>45°,∴点G在第一象限.
当点F在点E的左边时,如图3—1所示:
由(2)可知直线PC的解析式为y=﹣x﹣3,且∠PDE= 45°,OD=3,
∵PE⊥PC,
∴∠PED= 45°,∠EHO= 45°,
∴ PE=PD,∠PEF= 135°,∠GHO= 135°.
∵∠EFP+∠PGO=45°,∠GOH+∠PGO=45°,
∴∠EFP=∠GOH.
在△PFE和△GOH中,
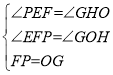 ,
,
∴△PFE≌△GOH(AAS),
∴EF=HO=11.
∴EO=HO=11,
∴DE=8,
∴点P的横坐标距离原点的距离为7,即点P的横坐标为﹣7,
将﹣7代入直线PC的解析式为y=﹣x﹣3,
则点P的纵坐标为4,
∴点P的坐标为(-7,4).
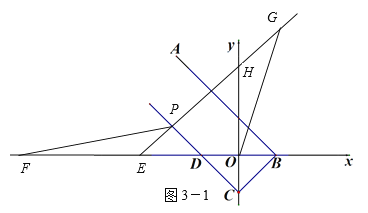
当点F在点E的左边时,如图3-2所示:
同理可证得FD=HO=EO,
∵ EF=11,
∴ EO+OF=11,
∴ EO+FD-OD=11,
∴ 2ED=11+3,
∴ ED=7,
即点P的横坐标为﹣5,
将﹣5代入直线PC的解析式为y=﹣x﹣3,
则点P的纵坐标为2,
∴点P的坐标为(-5,2).
所以点P坐标为(-5,2)或(-7,4).


科目:初中数学 来源: 题型:
【题目】小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,按下任意一个开关均可打开对应的一盏电灯,因刚搬进新房不久,不熟悉情况.
(1)若小明任意按下一个开关,则下列说法正确的是 .
A.小明打开的一定是楼梯灯
B.小明打开的可能是卧室灯
C.小明打开的不可能是客厅灯
D.小明打开走廊灯的概率是![]()
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB>AC,点D、E分别是边AB、AC的中点,点F在BC边上,连接DE、DF、EF,则添加下列哪一个条件后,仍无法判断△FCE与△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
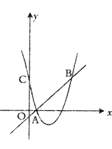
(1)求![]() 的值和抛物线的解析式;
的值和抛物线的解析式;
(2)直接写出方程![]() 的解;
的解;
(3)点![]() 是抛物线
是抛物线![]() 对称轴上的一个动点,当
对称轴上的一个动点,当![]() 的值最小时,判断
的值最小时,判断![]() 的形状.
的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为18,BP=4,则AB的长为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红和小华都想去参加学校组织的演讲比赛,但现在名额只有一个,于是小英想出了一个办法:让小红和小华分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被四等分),在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则小红去;若指针所指的两个数字之和为奇数,则小华去,你认为这个方法公平吗?请说明理由.
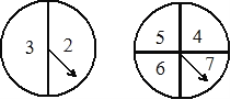
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点B,与直线y=x交于点C.
x+2与x轴交于点A,与y轴交于点B,与直线y=x交于点C.

(1)求A,B,C三点的坐标;
(2)求△AOC的面积;
(3)已知点P是x轴正半轴上的一点,若△COP是等腰三角形,直接写点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com