练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知关于的一元二次方程.

    （1）当时，利用根的判别式判断方程根的情况；

    （2）若方程有两个相等的实数根，请写出一组满足条件的的值，并求出此时方程的根.

    【答案】（1）原方程有两个不相等的实数根；（2）a=2,b=2,x1=x2=-.

    【解析】

    （1）由方程的系数结合根的判别式、b=a+1，可得出△=a2+1＞0，进而可找出方程ax2+bx+=0有两个不相等实数根；

    （2）由根的判别式△=b2-2a=0，可得出：若b=2，a=2，则原方程为2x2+2x+=0，解之即可得出结论．

    （1）

    ∵

    ∴

    ∵

    ∴，

    ∴

    ∴

    ∴原方程有两个不相等的实数根.

    （2）∵方程有两个相等的实数根，

    ∴b2-2a=0,即b2=2a,

    取a=2,b=2,

    则方程为2x2+2x+=0,

    ∴x1=x2=-.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了改善小区环境，某小区决定要在一块一边靠墙（墙长25m）的空地上修建一个矩形绿化带ABCD，绿化带一边靠墙，另三边用总长为40m的栅栏围住（如图）．若设绿化带的BC边长为x m，绿化带的面积为y m2．

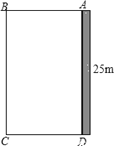
    （1）求y与x之间的函数关系式，并写出自变量x的取值范围；

    （2）当x为何值时，满足条件的绿化带的面积最大．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：四边形ABCD中，AC为对角线，∠DAC＝∠BCA，且AD＝BC，CD⊥AD于点D。

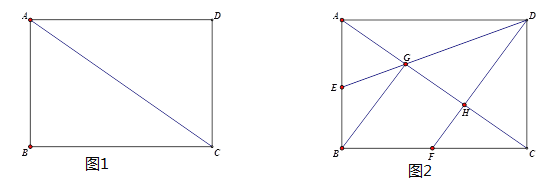
    （1）如图1，求证：四边形ABCD是矩形。

    （2）如图2，点E和点F分别为边AB和边BC的中点，连接DE、DF分别交AC于点G和点H，连接BG，在不连接其它线段的情况下，请写出所有面积是△FHC面积的2倍的所有三角形。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

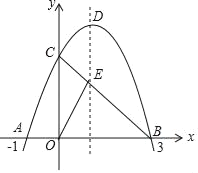
    【题目】如图，已知抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点C，连接BC交抛物线的对称轴于点E、D是抛物线的顶点．

    （1）求此抛物线的解析式；

    （2）求点C和点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

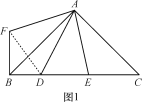
    【题目】(1)如图1，△ABC中，∠BAC＝90°，AB＝AC，D，E在BC上，∠DAE＝45°，为了探究BD，DE，CE之间的等量关系，现将△AEC绕A顺时针旋转90°后成△AFB，连接DF，经探究，你所得到的BD，DE，CE之间的等量关系式是 ；(无须证明)

    (2)如图2，在△ABC中，∠BAC＝120°，AB＝AC，D，E在BC上，∠DAE＝60°，∠ADE＝45°，试仿照(1)的方法，利用图形的旋转变换，探究BD，DE，CE之间的等量关系，并证明你的结论．

    　　　　　　

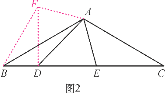
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如下图所示，且关于x的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论：①b2-4ac>0；②abc<0；③m>2.其中，正确结论的个数是

    A. 0 B. 1 C. 2 D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】安徽郎溪农民张大伯为了致富奔小康，大力发展家庭养殖业.他准备用长的木栏围一个矩形的羊圈，为了节约材料同时要使矩形的面积最大，他利用了自家房屋一面长的墙，设计了如图所示的一个矩形羊圈.

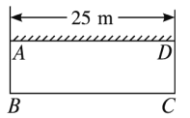
    （1）请你求出张大伯的矩形羊圈的面积；

    （2）请你判断他的设计方案是否合理？如果合理，直接答合理；如果不合理又该如何设计？并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C是以AB为直径的半圆O的三等分点，AC=2，则图中阴影部分的面积是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：

    （1）在图中确定该圆弧所在圆的圆心D点的位置，并写出点D点坐标为________．

    （2）连接AD、CD，求⊙D的半径及的长；

    （3）有一点E（6，0），判断点E与⊙D的位置关系．

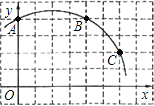
    查看答案和解析>>

    同步练习册答案