
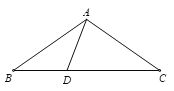
【题目】如图,在△ABC中,D在BC上,若AD=BD,AB=AC=CD,则∠BAC=_________
【答案】108°
【解析】
由AD=BD得到∠BAD=∠DBA,由AB=AC=CD得到∠CAD=∠CDA,∠DBA=∠C,再由三角形外角性质得到∠CAD=∠CDA=2∠DBA,从而可以推出∠BAC=3∠DBA,再根据三角形的内角和定理可求出∠DBA的度数,再求出∠BAC的度数.
解:设∠DBA的度数为![]() ,
,
∵AD=BD,
∴ ∠BAD=∠DBA =![]() .
.
∵ AB=AC=CD,
∴ ∠CAD=∠CDA,∠DBA=∠C=![]() .
.
∵ 由三角形外角和性质可得:∠CAD=∠CDA=2∠DBA=2![]() ,
,
∴ ∠BAC=∠DBA +∠CAD =3∠DBA=3![]() .
.
∵∠BAC+∠DBA +∠C=180°,
∴3![]() +
+![]() +
+![]() =180°,
=180°,
∴5![]() =180°,
=180°,
∴![]() =36°,
=36°,
∴∠BAC=3![]() =108°.
=108°.
故答案为:108°.


科目:初中数学 来源: 题型:
【题目】(1)如图 1,已知正方形 ABCD,点 E 在 BC 上,点 F 在 DC 上,且∠EAF=45°,则有 BE+DF= .若 AB=4,则△CEF 的周长为 .
(2)如图 2,四边形 ABCD 中,∠BAD=∠C=90°,AB=AD,点 E,F 分别在 BC,CD 上,且∠EAF=45°,试判断 BE,EF,DF 之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=![]() (BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
(BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
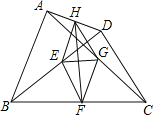
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
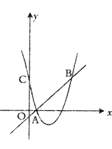
【题目】如图,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值和抛物线的解析式;
的值和抛物线的解析式;
(2)直接写出方程![]() 的解;
的解;
(3)点![]() 是抛物线
是抛物线![]() 对称轴上的一个动点,当
对称轴上的一个动点,当![]() 的值最小时,判断
的值最小时,判断![]() 的形状.
的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点D、E分别在AB、BC上,BD=CE,连接AE,CD交于点O
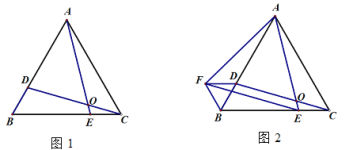
(1)如图1,求证:CD=AE;
(2)如图2,作等边△AEF,连接BF,DF.直接写出图2中所有120度的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
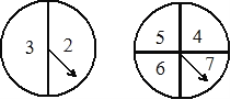
【题目】红和小华都想去参加学校组织的演讲比赛,但现在名额只有一个,于是小英想出了一个办法:让小红和小华分别转动下图的甲、乙两个转盘(转盘甲被二等分、转盘乙被四等分),在两个转盘都停止转动后,若指针所指的两个数字之和为偶数,则小红去;若指针所指的两个数字之和为奇数,则小华去,你认为这个方法公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
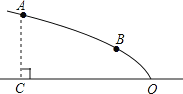
【题目】如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O落在水平面上,对称轴是水平线OC.点A、B在抛物线造型上,且点A到水平面的距离AC=4米,点B到水平面距离为2米,OC=8米.
(1)请建立适当的直角坐标系,求抛物线的函数解析式;
(2)为了安全美观,现需在水平线OC上找一点P,用质地、规格已确定的圆形钢管制作两根支柱PA、PB对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点P?(无需证明)
(3)为了施工方便,现需计算出点O、P之间的距离,那么两根支柱用料最省时点O、P之间的距离是多少?(不写求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
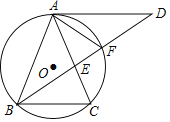
【题目】如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)求∠DAF的度数;
(2)求证:AE2=EFED;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com