
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D.
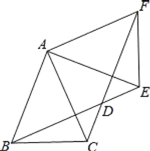
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
【答案】(1)见解析;(2)CD=2![]() ﹣2.
﹣2.
【解析】
(1)根据旋转的性质得到AE=AF=AB=AC=2,∠EAF=∠BAC=45°,然后根据“边角边”证明△ABE≌△ACF,之后根据全等三角形性质得出结论即可。
(2)根据菱形的性质得出DF=AF=2,DF∥AB,再根据平行线 性质证明∠1=∠BAC=45°,此时则可判定断△ACF为等腰直角三角形,之后进一步求解即可。
(1)证明:如图
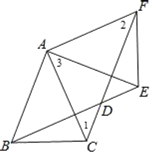 ,
,
∵△AEF是由△ABC绕点A按逆时针方向旋转得到的,
∴AE=AF=AB=AC=2,∠EAF=∠BAC=45°,
∴∠BAC+∠3=∠EAF+∠3,
即∠BAE=∠CAF,在△ABE和△ACF中:
∵AB=AC,∠BAE=∠CAF,AE=AF,
∴△ABE≌△ACF(SAS),
∴BE=CF;
(2)解:如图
 ,
,
∵四边形ABDF为菱形,
∴DF=AF=2,DF∥AB,
∴∠1=∠BAC=45°,
∴△ACF为等腰直角三角形,
∴CF=![]() AF=2
AF=2![]() ,
,
∴CD=CF﹣DF=2![]() ﹣2.
﹣2.


科目:初中数学 来源: 题型:
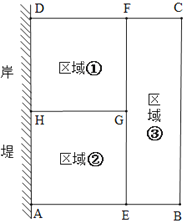
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且AE:BE=2:1.设BC的长度是![]() 米,矩形区域ABCD的面积为
米,矩形区域ABCD的面积为![]() 平方米.
平方米.
(1)求![]() 与
与![]() 之间的函数关系式,并注明自变量
之间的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)![]() 取何值时,
取何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
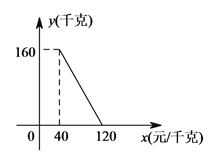
【题目】某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)根据图象,求y与x的函数关系式;
(2)商店想在销售成本不超过3000元的情况下,使销售利润达到2400元,问销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“我要上春晚”进入决赛阶段,最终将有甲、乙、丙、丁4名选手进行决赛的终极较量,决赛分3期进行,每期比赛淘汰1名选手,最终留下的歌手即为冠军.假设每位选手被淘汰的可能性都相等.
(1)甲在第1期比赛中被淘汰的概率为 ;
(2)用树状图法或表格法求甲在第2期被淘汰的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为![]() 米,中午
米,中午![]() 时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方
时不能挡光. 如图,某旧楼的一楼窗台高1米,要在此楼正南方![]() 米处再建一幢新楼. 已知该地区冬天中午
米处再建一幢新楼. 已知该地区冬天中午![]() 时阳光从正南方照射,并且光线与水平线的夹角最小为
时阳光从正南方照射,并且光线与水平线的夹角最小为![]() °,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.
°,在不违反规定的情况下,请问新建楼房最高_____________米. (结果精确到1米.![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
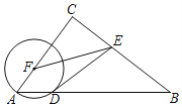
【题目】如图,Rt△ABC中,∠C=90°,AB=4![]() ,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为_______________.
,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2m+3)x+m2+2=0.
(1)若方程有实数根,求实数m的取值范围;
(2)若方程的两个根分别为x1、x2,且满足x12+x22=31+x1x2,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com