
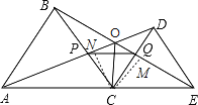
【题目】已知,如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,OC,以下四个结论:①AD=BE;②三角形CPQ是等边三角形;③AD⊥BC;④OC平分∠AOE其中正确的结论有______(把你认为正确的序号都填上).

【答案】①②④
【解析】
根据等边三角形的三边都相等,三个角都是60°,可以证明△ACD与△BCE全等,根据全等三角形对应边相等可得AD=BE,所以①正确;对应角相等可得∠CAD=∠CBE,然后证明△ACP与△BCQ全等,根据全等三角形对应角相等可得PC=PQ,从而得到△CPQ是等边三角形,所以②正确;再根据等腰三角形的性质可以找出相等的角,求出∠BOA=60°,根据三角形的内角和定理求出∠BPO不是90°,即可判断③;根据三角形面积公式求出CN=CM,根据角平分线性质即可判断④.
解:∵等边△ABC和等边△CDE,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴180°-∠ECD=180°-∠ACB,
即∠ACD=∠BCE,
在△ACD与△BCE中,
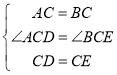 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,故①小题正确;
∵△ACD≌△BCE(已证),
∴∠CAD=∠CBE,
∵∠ACB=∠ECD=60°(已证),
∴∠BCQ=180°-60°×2=60°,
∴∠ACB=∠BCQ=60°,
在△ACP与△BCQ中,
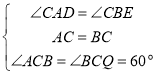 ,
,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,
∵∠PCQ=180°-60°-60°=60°,
∴△PCQ是等边三角形,故②小题正确;
∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∴∠AOB=∠DAC+∠CEB=∠DAC+∠ADC=∠DCE=60°,
∵○CBE+∠CEB=∠ACB=60°,而BC≠CE,
∴∠CPB≠30°,
∴∠BPD≠90°,
∴③错误;
过C作CM⊥BE于M,CN⊥AD于N,
∵△BCE≌△ACD,
∴S△BCE=S△ACD,BE=AD,
∴![]() ×BE×CM=
×BE×CM=![]() ×AD×CN,
×AD×CN,
∴CM=CN,
∴OC平分∠AOE,故④正确.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】李刚和父母一起从家到姑妈家去,两地相距![]() ,出发前汽车油箱里有
,出发前汽车油箱里有![]() 油,途中加油若干升,加油前后汽车都以
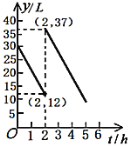
油,途中加油若干升,加油前后汽车都以![]() 的速度匀速行驶.已知油箱中剩余油量
的速度匀速行驶.已知油箱中剩余油量![]() 与行驶时间
与行驶时间![]() 之间的关系如图所示.则下列说法:①汽车行驶了
之间的关系如图所示.则下列说法:①汽车行驶了![]() 后加油;②途中加油
后加油;②途中加油![]() ;③加油前油箱中剩余油量
;③加油前油箱中剩余油量![]() 与行驶时间
与行驶时间![]() 之间的函数关系式是
之间的函数关系式是![]() ;④汽车加油后还可行驶
;④汽车加油后还可行驶![]() ;⑤汽车到达姑妈家,油箱中还剩余
;⑤汽车到达姑妈家,油箱中还剩余![]() 油.其中全部正确的是( )
油.其中全部正确的是( )
A.①④⑤B.①③④C.②⑤D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |

请根据以上信息解答下列问题:
(1)填空:m= ______ ,n= ______ ;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,C在EF上,AD∥BC,DE∥BF,AE=CF.
(1)求证:四边形ABCD是平行四边形;
(2)直接写出图中所有相等的线段(AE=CF除外).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示在三角形△ABC中AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论中,①AB上一点与AC上一点到D的距离相等;②AD上任意一点到AB、AC的距离相等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的个数是
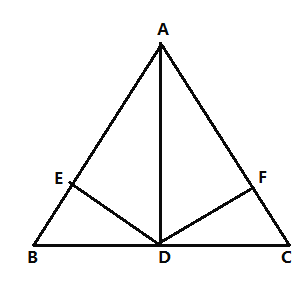
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是

A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万圣节两周前,某商店购进1000个万圣节面具,进价为每个6元,第一周以每个10元的价格售出200个;随着万圣节的临近,预计第二周若按每个10元的价格销售可售出400个,但商店为了尽快减少库存,决定单价降价x元销售![]() 根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价
根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价![]() ;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
![]() 当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
![]() 如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2 - 2(1-m)x+m2的两实数根为x1,x2.
(1)求m的取值范围;
(2)设![]() ,当m为何值时,y有最小值,求y的最小值.
,当m为何值时,y有最小值,求y的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com