
【题目】附加题:如图,直线![]() :
:![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,经过
,经过![]() 、
、![]() 两点的抛物线
两点的抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() .
.
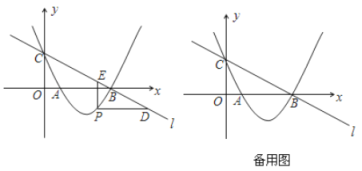
(1)求该抛物线的解析式;
(2)若点![]() 在直线
在直线![]() 下方的抛物线上,过点
下方的抛物线上,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形能否构成平行四边形?若能,求出点
为顶点的四边形能否构成平行四边形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
【答案】(1)![]() ;(2)3;(3)能,
;(2)3;(3)能,![]() 或
或![]()
【解析】
(1)先求点B与点C的坐标,再将求得的坐标代入抛物线求解方程组即得.
(2)由(1)先设点![]() 坐标,其中点P的横坐标为m
坐标,其中点P的横坐标为m![]() ,再将PD+PE用含m的式子表示,最后利用二次函数的性质求出最大值;
,再将PD+PE用含m的式子表示,最后利用二次函数的性质求出最大值;
(3)当AB为平行四边形的边时,设点![]() 的坐标,进而利用
的坐标,进而利用![]() 列方程求解即得;当AB为平行四边形的对角线时,先求
列方程求解即得;当AB为平行四边形的对角线时,先求![]() 交
交![]() 于点
于点![]() 的坐标,再利用
的坐标,再利用![]() 列方程求解即得.
列方程求解即得.
解:(1)∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,
,
∴![]() 、
、![]() ,
,
∵![]() 、
、![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() 解得:
解得: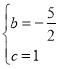 ,
,
∴抛物线的解析式为![]()
(2)设![]()
∵![]() 轴,
轴,![]() 轴,点
轴,点![]() 及点
及点![]() 都在直线
都在直线![]() 上,
上,
∴![]() ,
,![]() ,
,
∴![]()
![]()
![]()
∴当![]() 时,
时,![]() 的最大值是3;
的最大值是3;
(3)能,理由如下:
由![]() ,令
,令![]() ,解得:
,解得:![]() 或
或![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,
若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形能构成平行四边形,
为顶点的四边形能构成平行四边形,
①当以![]() 为边时,则
为边时,则![]() 且
且![]()
设![]() ,则
,则![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() (与
(与![]() 重合,舍去),
重合,舍去),
∴![]()
②当以![]() 为对角线时,连接
为对角线时,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,
,![]() ,
,
设![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
如图,作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,则
,则![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() (与
(与![]() 重合,舍去),
重合,舍去),
∴![]() ,
,
综上所述,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形能构成平行四边形,此时点
为顶点的四边形能构成平行四边形,此时点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )

A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的点,记△AOB内部(不包括边界)的整点个数为m.当m=6时,点B的横坐标a的取值范围是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆及升旗台的剖面和教学楼的剖面在同一平面上,旗杆与地面垂直,在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°,升旗台底部到教学楼底部的距离DE=7米,升旗台坡面CD的坡度i=1:0.75,坡长CD=2米,若旗杆底部到坡面CD的水平距离BC=1米,求旗杆AB的高度约为多少?(保留一位小数,参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.6)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的两直角边
的两直角边![]() ,
,![]() 分别在
分别在![]() 轴的负半轴和
轴的负半轴和![]() 轴的正半轴上,
轴的正半轴上,![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,且顶点在直线
,且顶点在直线![]() 上.
上.
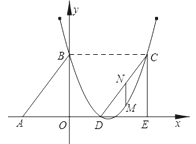
(1)求抛物线对应的函数关系式;
(2)若![]() 是由
是由![]() 沿
沿![]() 轴向右平移得到的,当四边形
轴向右平移得到的,当四边形![]() 是菱形时,试判断点
是菱形时,试判断点![]() 和点
和点![]() 是否在该抛物线上,并说明理由;
是否在该抛物线上,并说明理由;
(3)在(2)的条件下,若![]() 点是
点是![]() 所在直线下方抛物线上的一个动点,过点
所在直线下方抛物线上的一个动点,过点![]() 作
作![]() 平行于
平行于![]() 轴交
轴交![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长度为
的长度为![]() .求
.求![]() 与
与![]() 之间的函数关系式,写出自变量
之间的函数关系式,写出自变量![]() 的取值范围,并求
的取值范围,并求![]() 取最大值时,点
取最大值时,点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则![]() 的值为___________.
的值为___________.
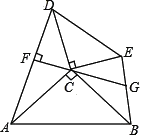
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com