
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.
(1)求证:△AOC≌△CEB;
(2)求△ABD的面积.
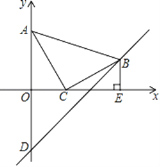
【答案】(1)详见解析;(2)6.
【解析】
(1)根据等腰直角三角形的性质,可得AC=BC,∠ACB=90°,根据余角的性质,可得∠OAC=∠BCE,根据AAS,可得答案;
(2)根据全等三角形的性质,可得B点坐标,根据待定系数法,可得b的值,根据三角形的面积公式,可得答案.
(1)证明:∵BE⊥CE,
∴∠BEC=90°,
∵△ABC是等腰直角三角形,
∴AC=BC,∠ACB=90°,
∵∠O=∠ACB=90°,
∴∠OAC+∠ACO=90°,∠ACO+∠BCE=90°,
∴∠OAC=∠BCE,
在Rt△AOC和Rt△CEB中,
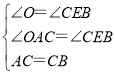 ,
,
∴Rt△AOC≌Rt△CEB(AAS);
(2)如图:作BF⊥y轴于F点,
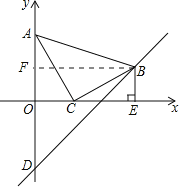
∵Rt△AOC≌Rt△CEB,
∴CE=OA=2,BE=OC=1,
∴OE=CC+CE=1+2=3,
即B(3,1),BF=3,
将B点坐标代入y=x+b,得3+b=1,
解得b=-2,
直线BD的解析式为y=x-2,
当x=0时,y=-2,即D(0,-2),
S△ABD=![]() ADBF=
ADBF=![]() ×[2-(-2)]×3=6.
×[2-(-2)]×3=6.


科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图.
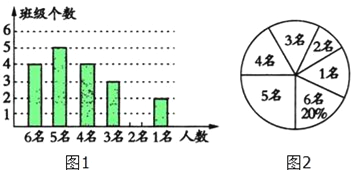
(1)求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“端午”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
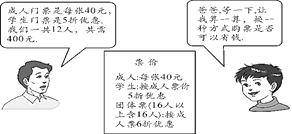
(1)他们共去了几个成人,几个学生?
(2)请你帮助算算,小明用更省钱的购票方式是指什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En.则OnEn= AC.(用含n的代数式表示)
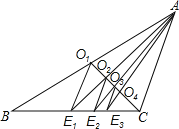
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AB=5,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
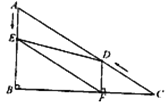
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.
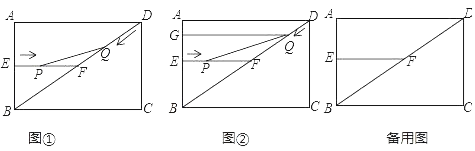
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小兵、小英三人的家和学校在同一条东西走向的大街上,星期天班主任到这三位学生家进行家访,班主任从学校出发先向东走0.5千米到小明家,后又向东走1.5千米到小兵家,再向西走5千米到小英家,最后回到学校。
(1)以学校为原点,画出数轴并在数轴上分别表示出小明、小兵、小英三人家的位置。
(2)小明家距离小英家多远?
(3)这次家访,班主任共走了多少千米路程?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com