
【题目】如图,y轴上有一点A(0,1),点B是x轴上一点,∠ABO=60°,抛物线y=﹣![]() x2+
x2+![]() +3
+3![]() 与x轴交于C、D两点(点C在点D的左侧).
与x轴交于C、D两点(点C在点D的左侧).
(1)将点C向右平移![]() 个单位得到点E,过点E作直线l⊥x轴,点P为y轴上一动点,过点P作PQ⊥y轴交直线l于点Q,点K为抛物线上第一象限内的一个动点,当△ABK面积最大时,求KQ+QP+PE的最小值,及此时点P的坐标;
个单位得到点E,过点E作直线l⊥x轴,点P为y轴上一动点,过点P作PQ⊥y轴交直线l于点Q,点K为抛物线上第一象限内的一个动点,当△ABK面积最大时,求KQ+QP+PE的最小值,及此时点P的坐标;
(2)在(1)的条件下,将线段PE绕点P逆时针旋转90°后得线段PE′,问:在第一象限内是否存在点S,使得△SPE'是有一个角为60°,且以线段PE′为斜边的直角三角形,若存在请直接写出所有满足条件的点S,若不存在,请说明理由.

【答案】(1)7,(0,![]() );(2)存在,S2(
);(2)存在,S2(![]() ,
,![]() ),S3(
),S3(![]() ,
,![]() ),S4(
),S4(![]() ,
,![]() )
)
【解析】
(1)解直角三角形求出OB,求出直线AB的解析式,构建方程组转化为一元二次方程,利用△=0,确定点K的坐标,如图1中,点K向右平移一个单位得到K′(2,3![]() ),连接K′E,则KQ+QP+PE的最小值=K′E+QP,再求出EK′的解析式即可求出点P的坐标.
),连接K′E,则KQ+QP+PE的最小值=K′E+QP,再求出EK′的解析式即可求出点P的坐标.
(2)由(1)可知E(﹣1,0),P(0,![]() ),将PE绕点P逆时针旋转90°得到PE′,可得E′(
),将PE绕点P逆时针旋转90°得到PE′,可得E′(![]() ,
,![]() ﹣1),以PE′为边作等边三角形PE′N,等边三角形PE′M,可得M(0,
﹣1),以PE′为边作等边三角形PE′N,等边三角形PE′M,可得M(0,![]() ﹣2),N(
﹣2),N(![]() ,
,![]() +1),此时四边形PME′N是菱形,取各边的中点S1,S2,S3,S4,可得△PE′S1,△PE′S2,△PE′S3,△PE′S4都是含有60°且以PE′为斜边的直角三角形,再根据点S在第一象限,即可解决问题.
+1),此时四边形PME′N是菱形,取各边的中点S1,S2,S3,S4,可得△PE′S1,△PE′S2,△PE′S3,△PE′S4都是含有60°且以PE′为斜边的直角三角形,再根据点S在第一象限,即可解决问题.
解:(1)由题意在Rt△AOB中,∵OA=1,∠ABO=60°,
∴BO=![]() OA=
OA=![]() ,
,
∴B(![]() ,0),
,0),
设直线AB的解析式为y=kx+b,把A(0,1),B(![]() ,0)代入可得
,0)代入可得
 ,解得
,解得 ,
,
∴直线AB的解析式为y=﹣![]() x+1,
x+1,
对于抛物线y=﹣![]() x2+
x2+![]() x+3
x+3![]() ,令y=0,得到x2﹣x﹣3=0,解得x=
,令y=0,得到x2﹣x﹣3=0,解得x=![]() ,
,
则C(![]() ,0),D(
,0),D(![]() ,0),
,0),
将点C向右平移![]() 个单位得到E(﹣1,0),
个单位得到E(﹣1,0),
设平行于AB的解析式为y=﹣![]() x+m,
x+m,
由 ,
,
消去y得到﹣![]() x2+2
x2+2![]() x+3
x+3![]() ﹣m=0,
﹣m=0,
由△=0得到m=﹣4![]() ,xk=﹣1,yk=3
,xk=﹣1,yk=3![]() ,
,
则K(1,3![]() ),
),
如图1中,点K向右平移一个单位得到K′(2,3![]() ),连接K′E,
),连接K′E,

则KQ+QP+PE的最小值=K′E+QP=![]() ,
,
∵E(﹣1,0),K′(2,3![]() ),
),
∴直线EK′的解析式为y=![]() x+
x+![]() ,
,
∴P(0,![]() ).
).
(2)如图2中,

由(1)可知E(﹣1,0),P(0,![]() ),将PE绕点P逆时针旋转90°得到PE′,可得E′(
),将PE绕点P逆时针旋转90°得到PE′,可得E′(![]() ,
,![]() ﹣1),
﹣1),
以PE′为边作等边三角形PE′N,等边三角形PE′M,
可得M(0,![]() ﹣2),N(
﹣2),N(![]() ,
,![]() +1),此时四边形PME′N是菱形,取各边的中点S1,S2,S3,S4,可得△PE′S1,△PE′S2,△PE′S3,△PE′S4都是含有60°且以PE′为斜边的直角三角形,
+1),此时四边形PME′N是菱形,取各边的中点S1,S2,S3,S4,可得△PE′S1,△PE′S2,△PE′S3,△PE′S4都是含有60°且以PE′为斜边的直角三角形,
∵点S在第一象限,
∴满足条件的点S2(![]() ,
,![]() ),S3(
),S3(![]() ,
,![]() ),S4(
),S4(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,C为BD上一点,使得CA=CD,过点C作CE∥AD交AB于点E,过点D作DF⊥AD交AC的处长线于点F.
(1)若CD=3,求AF的长;
(2)若∠B=30°,∠ADC=40°,求证:AC=EC.

查看答案和解析>>
科目:初中数学 来源: 题型:
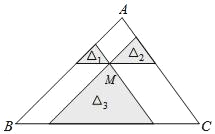
【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知点A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )

A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级261位学生参加期末考试,某班35位学生的语文成绩、数学成绩与总成绩在全年级中排名情况如图1和图2所示,甲、乙、丙为该班三位学生.

从这次考试成绩看,①在甲、乙两人中,总成绩名次靠前的学生是______;
②在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是______.
你选择的理由是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1979年,在邓小平同志的提议下,第五届全国人大常委会第六次会议决定每年3月12日为我国的植树节,今年是第40个植树节,明德中学师生积极响应国家“绿水青山就是金山银山”的号召,到距学校20千米的山上义务植树,老师和男生骑自行车先走,走了16千米后,女生乘汽车拉着工具、树苗出发,结果同时到达.已知汽车的速度比自行车的速度快60千米/小时,求两种车的速度各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com